Home » Mathematics » Calculus BC » Logistic Growth

John Zhu

John Zhu

Logistic Growth

Slide Duration:

Table of Contents

Section 1: Prerequisites
Parametric Curves

10m 10s

Intro
0:00
Parametric Equations
0:23
Familiar Functions
0:32
Parametric Equation/ Function
0:56
Example 1: Graph Parametric Equation
1:48
Example 2
4:30
Example 3
6:01
Example 4
7:12
Example 5
8:10
Polar Coordinates

14m 54s

Intro
0:00
Polar Coordinates
0:09
Definition
0:11
Example
0:23
Converting Polar Coordinates
1:49
Example: Convert Polar Equation to Cartesian Coordinates
3:06
Example: Convert Polar Equation to Cartesian Coordinates
5:21
Example: Find the Polar Representation
6:51
Example: Find the Polar Representation
8:39
Example: Sketch the Graph
10:02
Vector Functions

12m 5s

Intro
0:00
Vector Functions
0:11
2 Parts
0:18
Example 1
1:44
Example 2
3:52
Example 3
4:59
Example 4
6:03
Example 5
8:00
Example 6
9:23
Example 7
10:16
Section 2: Differentiation
Parametric Differentiation

13m 15s

Intro
0:00
Parametric Differentiation
0:15
Example 1
1:16
Example 2
1:54
Example 3
3:15
Example 4
4:59
Parametric Differentiation: Position, Speed & Acceleration
7:45
Example 5
8:32
Example 6
10:37
Polar Differentiation

10m 14s

Intro
0:00
Polar Differentiation
0:11
Goal
0:13
Method
0:24
Example 1
0:52
Example 2
4:27
Example 3
7:03
L'Hopital's Rule

6m 43s

Intro
0:00
L'Hopitals Rule
0:09
Conditions
0:14
Limit
0:36
Example 1
1:21
Example 2
2:38
Example 3
4:09
Example 4
5:01
Section 3: Integration
Integration By Parts

19m 4s

Intro
0:00
Integration by Parts
0:12
Formula
0:31
How It's Derived From Product Rule
1:09
Integration by Parts: Rules to Follow
3:24
Recap of the Rules
4:13
Example 1
4:29
Example 2
7:04
Example 3
8:40
Example 4
13:48
Example 5
15:36
Integration By Partial Fractions

22m 4s

Intro
0:00
Integration by Partial Fractions: Goal
0:08
Example 1
2:10
Example 2
7:10
Example 3
10:06
Example 4
14:23
Example 5
16:26
Improper Integrals

19m 1s

Intro
0:00
Improper Integrals
0:06
3 Steps
1:11
Example 1
1:46
Example 2
3:20
Example 3
6:05
Example 4
9:02
Example 5
11:21
Example 6
15:54
Section 4: Applications of Integration
Logistic Growth

19m 16s

Intro
0:00
Logistic Growth Function
0:07
Defining Variables
0:40
Equation Parts
1:51
Logistic Growth
2:04
Example 1
2:59
Example 2
7:13
Example 3
11:29
Example 4
15:21
Arc Length for Parametric & Polar Curves

17m 40s

Intro
0:00
Arc Length
0:13
Arc Length of a Normal Function
0:24
Example
1:27
Example 2: Arc Length for Parametric Curves
3:31
Example 3: Arc Length for Parametric Curves
4:23
Example 4: Arc Length for Parametric Curves
8:05
Example 5: Arc Length for Parametric Curves
12:22
Example 6: Arc Length for Polar Curves
15:36
Example 7: Arc Length for Polar Curves
16:03
Area for Parametric & Polar Curves

4m 33s

Intro
0:00
Area for Parametric Curves: Parametric Function
0:10
Example 1: Area for Parametric Curves
0:35
Area for Parametric Curves: Polar Function
2:50
Example 2: Area for Polar Curves
3:18
Section 5: Sequences, Series, & Approximations
Definition & Convergence

7m 10s

Intro
0:00
Sequences: Definition
0:09
Definition
0:31
Example 1
1:07
Sequences: Convergence
2:02
Example 1
2:52
Example 2
3:36
Example 3
4:47
Example 4
6:16
Geometric Series

10m 59s

Intro
0:00
Geometric Series
0:07
Definition
0:24
Expanded Form
0:39
Convergence Rules
1:00
Example 1: Convergence
1:22
Example 2: Convergence
2:36
Example 3: Convergence
3:45
Sum of Series
5:04
Sum of First n Terms
5:14
Sum of Series
5:24
Example 1: Sum of Series
5:39
Example 2: Sum of Series
7:15
Example 3: Sum of Series
8:24
Example 4: Sum of Series
9:36
Harmonic & P Series

3m 58s

Intro
0:00
Harmonic Series
0:08
P-Series
1:17
Example 1: P-Series Test
2:22
Example 2: P-Series Test
3:06
Integral Test

11m 31s

Intro
0:00
Integral Test
0:09
Example 1
0:54
Example 2
4:00
Example 3
7:59
Example 4
9:47
Comparison Test

7m 47s

Intro
0:00
Comparison Test
0:10
Example 1
1:07
Example 2
2:33
Example 3
4:20
Example 4
6:29
Limit Comparison Test

9m 40s

Intro
0:00
Limit Comparison Test
0:09
Conditions
0:31
Example 1
1:01
Example 2
2:53
Example 3
4:15
Example 4
6:19
Ratio Test

11m 20s

Intro
0:00
Ratio Test
0:09
Example 1
0:57
Example 2
2:55
Example 3
6:27
Example 4
8:36
Alternating Series

9m 11s

Intro
0:00
Alternating Series
0:08
Convergence Test
0:59
Example 1
1:27
Example 2
2:42
Example 3
4:57
Example 4
6:37
Absolute Convergence

7m 13s

Intro
0:00
Absolute Convergence
0:12
Example 1
0:52
Example 2
3:42
Example 3
5:21
Power Series Convergence

12m 52s

Intro
0:00
Power Series
0:09
Definition
0:19
Radius & Interval of Convergence
2:07
Example 1
2:28
Example 2
4:18
Example 3
6:20
Example 4
9:11
Taylor Series

15m 11s

Intro
0:00
Taylor Series
0:06
MacLaurin Series
0:45
Example 1
1:02
Example 2
2:45
Example 3
6:04
Example 4
8:23
Example 5
11:49
Power Series Operations

16m 40s

Intro
0:00
Operations
0:07
Example 1: Substitution
1:05
Example 2: Substitution
3:41
Example 3: Differentiation/ Integration
5:39
Example 4: Differentiation/ Integration
9:55
Example 5: Multiplying/ Dividing
12:32
Example 6: Multiplying/ Dividing
14:50
Lagrange Error

7m 9s

Intro
0:00
Power Series: Lagrange Error
0:06
Lagrange Remainder
0:21
Lagrange Error Bound
0:50
Example 1
1:06
Example 2
3:27
Section 6: Practice Test
AP Calc BC Practice Test Section 1: Multi Choice Part 1

15m 45s

Intro
0:00
Practice Problem 1
0:10
Practice Problem 2
1:19
Practice Problem 3
2:33
Practice Problem 4
5:25
Practice Problem 5
6:32
Practice Problem 6
9:11
Practice Problem 7
11:31
Practice Problem 8
13:08
Practice Problem 9
14:16
AP Calc BC Practice Test Section 1: Multi Choice Part 2

21m 38s

Intro
0:00
Practice Problem 10
0:12
Practice Problem 11
3:03
Practice Problem 12
4:53
Practice Problem 13
6:56
Practice Problem 14
9:10
Practice Problem 15
12:17
Practice Problem 16
14:43
Practice Problem 17
16:18
Practice Problem 18
18:34
AP Calc BC Practice Test Section 1: Multi Choice Part 3

17m 31s

Intro
0:00
Practice Problem 19
0:09
Practice Problem 20
3:03
Practice Problem 21
4:07
Practice Problem 22
5:41
Practice Problem 23
8:48
Practice Problem 24
11:16
Practice Problem 25
12:53
Practice Problem 26
14:12
Practice Problem 27
15:21
AP Calc BC Practice Test Section 1: Multi Choice Part 4

14m 17s

Intro
0:00
Practice Problem 28
0:08
Practice Problem 29
1:19
Practice Problem 30
2:15
Practice Problem 31
4:19
Practice Problem 32
6:54
Practice Problem 33
8:13
Practice Problem 34
9:03
Practice Problem 35
10:21
Practice Problem 36
11:42
AP Calc BC Practice Test Section 1: Multi Choice Part 5

22m 45s

Intro
0:00
Practice Problem 37
0:10
Practice Problem 38
4:09
Practice Problem 39
7:21
Practice Problem 40
9:42
Practice Problem 41
11:35
Practice Problem 42
14:01
Practice Problem 43
15:50
Practice Problem 44
16:43
Practice Problem 45
19:35
AP Calc BC Practice Test Section 1: Free Response Part 1

9m 55s

Intro
0:00
Practice Problem 1a
0:08
Practice Problem 1b
1:30
Practice Problem 1c
3:08
Practice Problem 2a
3:50
Practice Problem 2b
5:40
Practice Problem 2c
7:24
AP Calc BC Practice Test Section 1: Free Response Part 2

10m 8s

Intro
0:00
Practice Problem 3a
0:09
Practice Problem 3b
3:01
Practice Problem 4a
3:55
Practice Problem 4b
5:43
AP Calc BC Practice Test Section 1: Free Response Part 3

13m 58s

Intro
0:00
Practice Problem 5a
0:07
Practice Problem 5b
2:21
Practice Problem 5c
4:21
Practice Problem 6a
6:16
Practice Problem 6b
8:57
Practice Problem 6c
11:03
Loading...
This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Calculus BC
Bookmark & Share Embed

Share this knowledge with your friends!

Copy & Paste this embed code into your website’s HTML

Please ensure that your website editor is in text mode when you paste the code.
(In Wordpress, the mode button is on the top right corner.)
  ×
  • - Allow users to view the embedded video in full-size.
Since this lesson is not free, only the preview will appear on your website.

  • Discussion

  • Answer Engine

  • Study Guides

  • Practice Questions

  • Download Lecture Slides

  • Table of Contents

  • Related Books

Lecture Comments (2)

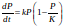
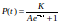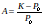
1 answer

Last reply by: Bharat Patel
Mon Mar 25, 2013 2:29 PM

Post by Raudel Ulloa on August 6, 2012

example 4, i got 152.9 pounds and the same k

Logistic Growth

  • Memorize:
    • ,
  • Solving logistic growth problems:
    • Apply formula with given variables
    • Solve unknown variables using given conditions
    • Complete growth model with solved variables
    • Evaluate function (growth model)

Logistic Growth

The population of Sedreville was 60 million in 2002 and 75 million in 2017.
Sedreville is speculated to have at most, 90 million denizens.
What is Sedreville's growth model?
  • Apply known values for the Logistic Growth model
  • K = 90
  • P(0) = 60
  • P(15) = 75
  • With P and K in terms of millions and t in terms of years
  • Solve for A
  • A = [(K − P0)/(P0)]
  • = [(90 − 60)/60]
  • = [1/3]
  • Find the k constant with P(15)
  • P(t) = [K/(Ae − kt + 1)]
  • 75 = [90/([1/3]e − 15k + 1)]
  • [1/3]e − 15k + 1 = [90/75]
  • [1/3]e − 15k = [6/5] − 1
  • [1/3]e − 15k = [1/5]
  • e − 15k = [3/5]
  • lne − 15k = ln[3/5]
  • − 15k = ln[3/5]
  • k = [(ln[3/5])/( − 15)]
  • k = 0.034
Definite the logistic growth model
P(t) = [90/([1/3]e − 0.034t + 1)]
What will the population be in 2020?
  • Find t in the context of 2020
  • 2020 − 2002 = 8
  • t = 8
  • Find P( 8 )
  • P(8) = [90/([1/3]e − 0.0348 + 1)]
≈ 71.8 million
What is the rate of the population growth for Sedreville at 2020?
[dP/dt] = kP( 1 − [P/K] ) = (0.034)(71.8)( 1 − [71.8/90] ) = 0.49
How long would it take, since 2002, for Sedreville to have 68 million denizens?
  • Find P(t) = 68 to solve for t
  • 68 = [90/([1/3]e − 0.034t + 1)]
  • [1/3]e − 0.034t + 1 = [90/68]
  • [1/3]e − 0.034t = [90/65] − 1
  • [1/3]e − 0.034t = [11/34]
  • e − 0.034t = [33/34]
  • lne − 0.034t = ln[33/34]
  • − 0.034t = ln[33/34]
  • t = [(ln[33/34])/( − 0.034)]
  • t = 0.878
  • 0.878*365 = 320.47
It will take about 320.47 days later for Sedreville to reach 68 million
Sedreville has a plan to restructure their city when their population reaches 85 million.
When do they restructure?
  • Find P(t) = 85 to solve for t
  • 85 = [90/([1/3]e − 0.034t + 1)]
  • [1/3]e − 0.034t + 1 = [90/85]
  • [1/3]e − 0.034t = [90/85] − 1
  • [1/3]e − 0.034t = [1/17]
  • e − 0.034t = [3/17]
  • lne − 0.034t = ln[3/17]
  • − 0.034t = ln[3/17]
  • t = [(ln[3/17])/( − 0.034)]
  • t = 51.02
  • 2002 + 51.02 ≈ 2053
Sedreville should restructure in 2053
The peaceful town of Cloudydale was in chaos when news brought forth that an infected kitten was carrying a lethal virus. On July 10th, a couple was found dead from the virus.
45 days later on August 24th, Cloudydale has an infected total of 2403 out of the 13578 townsfolk.
What is the growth model for the virus' carnage on Cloudydale?
  • Apply known values for the Logistic Growth model
  • K = 13578
  • P(0) = 2
  • P(45) = 2403
  • With t in terms of days
  • Solve for A
  • A = [(K − P0)/(P0)]
  • = [(13578 − 2)/2]
  • = 6788
  • Find the k constant with P(45)
  • 45 = [13578/(6788e − 45k + 1)]
  • 6788e − 45k + 1 = [13578/45]
  • 6788e − 45k = [13578/45] − [45/45]
  • 6788e − 45k = 300.73
  • e − 45k = 0.044
− 45k = − 3.11k = 0.07P(t) = [13578/(6788e − 0.07t + 1)]
Quarantine occur when 50% of the population is infected. When is the quarantine?
  • Determine 50% of the population
  • 50% of 13578 = 6789
  • Solve for P(t) = 6789
  • 6789 = [13578/(6788e − 0.07t + 1)]
  • 6788e − 0.07t + 1 = [13578/6789]
  • 6788e − 0.07t = 2 − 1
  • 6788e − 0.07t = 1
  • e − 0.07t = [1/6788]
  • lne − 0.07t = ln[1/6788]
  • − 0.07t = − 8.82
  • t = 126.04
The quarantine will occur about 126 days from July 10th
How much of the quarantine until 99% of Cloudydale is infected?
  • Determine 99% of the population
  • 99% of 13578 ≈ 13577
  • Solve for P(t) = 13577
  • 13577 = [13578/(6788e − 0.07t + 1)]
  • 6788e − 0.07t + 1 = [13578/13577]
  • 6788e − 0.07t = [13578/13577] − [13577/13577]
  • 6788e − 0.07t = [1/13577]
  • e − 0.07t = [1/13577]( [1/6788] )
  • lne − 0.07t = ln( [1/13577*6788] )
  • − 0.07t = − 18.34
  • t ≈ 262
  • 262 − 126 = 136
Cloudydale will become 99% infected 136 days after they're quarantined
Jerry just benched 155 pounds today. However, his personal best was 195 last year.
When he started working out 2 years ago, he could only bench 55 pounds.
What is Jerry's mathematical model for his progress?
  • Apply known values for the Logistic Growth model
  • K = 195
  • P(0) = 55
  • P(2) = 155
  • With P and K in terms of pounds, and t in terms of years.
  • Solve for A
  • A = [(K − P0)/(P0)]
  • = [(195 − 55)/55]
  • = [28/11]
  • Find the k constant with P(2)
  • 155 = [195/([28/11]e − 2k + 1)]
  • [28/11]e − 2k + 1 = [195/155]
  • [28/11]e − 2k = [195/155] − [155/155]
  • [28/11]e − 2k = [40/155]
  • e − 2k = [40/155]( [11/28] )
  • lne − 2k = ln( [40*11/155*28] )
  • − 2k = − 2.29
  • k = 1.145
P(t) = [195/([28/11]e − 1.15t + 1)]
How much longer until Jerry can bench 194 pounds?
  • Solve P(t) for 194
  • 194 = [195/([28/11]e − 1.15t + 1)]
  • [28/11]e − 1.15t + 1 = [195/194]
  • [28/11]e − 1.15t = [195/194] − [194/194]
  • [28/11]e − 1.15t = [1/194]
  • e − 1.15t = [1/194]( [11/11] )
  • lne − 1.15t = ln( [11/194*28] )
  • − 1.15t = − 6.20
  • t = [( − 6.20)/( − 1.15)]
  • ≈ 5.4
  • 5.4 − 3 = 2.4
It would take Jerry 2.4 more years to reach 194

*These practice questions are only helpful when you work on them offline on a piece of paper and then use the solution steps function to check your answer.

Answer

Logistic Growth

Lecture Slides are screen-captured images of important points in the lecture. Students can download and print out these lecture slide images to do practice problems as well as take notes while watching the lecture.

  • Intro 0:00
  • Logistic Growth Function 0:07
    • Defining Variables
    • Equation Parts
  • Logistic Growth 2:04
  • Example 1 2:59
  • Example 2 7:13
  • Example 3 11:29
  • Example 4 15:21

Related Books

Related Books

Educator®

Please sign in to participate in this lecture discussion.

Resetting Your Password?
or
Still having trouble? Contact us
OR

Start Learning Now

Our free lessons will get you started (Adobe Flash® required).
 Get immediate access to our entire library.

Membership Overview

  • Available 24/7. Unlimited Access to Our Entire Library.
  • Search and jump to exactly what you want to learn.
  • *Ask questions and get answers from the community and our teachers!
  • Practice questions with step-by-step solutions.
  • Download lecture slides for taking notes.
  • Track your course viewing progress.
  • Accessible anytime, anywhere with our Android and iOS apps.