

John Zhu
Absolute Convergence
Slide Duration:Table of Contents
Section 1: Prerequisites
Parametric Curves
10m 10s
- Intro0:00
- Parametric Equations0:23
- Familiar Functions0:32
- Parametric Equation/ Function0:56
- Example 1: Graph Parametric Equation1:48
- Example 24:30
- Example 36:01
- Example 47:12
- Example 58:10
Polar Coordinates
14m 54s
- Intro0:00
- Polar Coordinates0:09
- Definition0:11
- Example0:23
- Converting Polar Coordinates1:49
- Example: Convert Polar Equation to Cartesian Coordinates3:06
- Example: Convert Polar Equation to Cartesian Coordinates5:21
- Example: Find the Polar Representation6:51
- Example: Find the Polar Representation8:39
- Example: Sketch the Graph10:02
Vector Functions
12m 5s
- Intro0:00
- Vector Functions0:11
- 2 Parts0:18
- Example 11:44
- Example 23:52
- Example 34:59
- Example 46:03
- Example 58:00
- Example 69:23
- Example 710:16
Section 2: Differentiation
Parametric Differentiation
13m 15s
- Intro0:00
- Parametric Differentiation0:15
- Example 11:16
- Example 21:54
- Example 33:15
- Example 44:59
- Parametric Differentiation: Position, Speed & Acceleration7:45
- Example 58:32
- Example 610:37
Polar Differentiation
10m 14s
- Intro0:00
- Polar Differentiation0:11
- Goal0:13
- Method0:24
- Example 10:52
- Example 24:27
- Example 37:03
L'Hopital's Rule
6m 43s
- Intro0:00
- L'Hopitals Rule0:09
- Conditions0:14
- Limit0:36
- Example 11:21
- Example 22:38
- Example 34:09
- Example 45:01
Section 3: Integration
Integration By Parts
19m 4s
- Intro0:00
- Integration by Parts0:12
- Formula0:31
- How It's Derived From Product Rule1:09
- Integration by Parts: Rules to Follow3:24
- Recap of the Rules4:13
- Example 14:29
- Example 27:04
- Example 38:40
- Example 413:48
- Example 515:36
Integration By Partial Fractions
22m 4s
- Intro0:00
- Integration by Partial Fractions: Goal0:08
- Example 12:10
- Example 27:10
- Example 310:06
- Example 414:23
- Example 516:26
Improper Integrals
19m 1s
- Intro0:00
- Improper Integrals0:06
- 3 Steps1:11
- Example 11:46
- Example 23:20
- Example 36:05
- Example 49:02
- Example 511:21
- Example 615:54
Section 4: Applications of Integration
Logistic Growth
19m 16s
- Intro0:00
- Logistic Growth Function0:07
- Defining Variables0:40
- Equation Parts1:51
- Logistic Growth2:04
- Example 12:59
- Example 27:13
- Example 311:29
- Example 415:21
Arc Length for Parametric & Polar Curves
17m 40s
- Intro0:00
- Arc Length0:13
- Arc Length of a Normal Function0:24
- Example1:27
- Example 2: Arc Length for Parametric Curves3:31
- Example 3: Arc Length for Parametric Curves4:23
- Example 4: Arc Length for Parametric Curves8:05
- Example 5: Arc Length for Parametric Curves12:22
- Example 6: Arc Length for Polar Curves15:36
- Example 7: Arc Length for Polar Curves16:03
Area for Parametric & Polar Curves
4m 33s
- Intro0:00
- Area for Parametric Curves: Parametric Function0:10
- Example 1: Area for Parametric Curves0:35
- Area for Parametric Curves: Polar Function2:50
- Example 2: Area for Polar Curves3:18
Section 5: Sequences, Series, & Approximations
Definition & Convergence
7m 10s
- Intro0:00
- Sequences: Definition0:09
- Definition0:31
- Example 11:07
- Sequences: Convergence2:02
- Example 12:52
- Example 23:36
- Example 34:47
- Example 46:16
Geometric Series
10m 59s
- Intro0:00
- Geometric Series0:07
- Definition0:24
- Expanded Form0:39
- Convergence Rules1:00
- Example 1: Convergence1:22
- Example 2: Convergence2:36
- Example 3: Convergence3:45
- Sum of Series5:04
- Sum of First n Terms5:14
- Sum of Series5:24
- Example 1: Sum of Series5:39
- Example 2: Sum of Series7:15
- Example 3: Sum of Series8:24
- Example 4: Sum of Series9:36
Harmonic & P Series
3m 58s
- Intro0:00
- Harmonic Series0:08
- P-Series1:17
- Example 1: P-Series Test2:22
- Example 2: P-Series Test3:06
Integral Test
11m 31s
- Intro0:00
- Integral Test0:09
- Example 10:54
- Example 24:00
- Example 37:59
- Example 49:47
Comparison Test
7m 47s
- Intro0:00
- Comparison Test0:10
- Example 11:07
- Example 22:33
- Example 34:20
- Example 46:29
Limit Comparison Test
9m 40s
- Intro0:00
- Limit Comparison Test0:09
- Conditions0:31
- Example 11:01
- Example 22:53
- Example 34:15
- Example 46:19
Ratio Test
11m 20s
- Intro0:00
- Ratio Test0:09
- Example 10:57
- Example 22:55
- Example 36:27
- Example 48:36
Alternating Series
9m 11s
- Intro0:00
- Alternating Series0:08
- Convergence Test0:59
- Example 11:27
- Example 22:42
- Example 34:57
- Example 46:37
Absolute Convergence
7m 13s
- Intro0:00
- Absolute Convergence0:12
- Example 10:52
- Example 23:42
- Example 35:21
Power Series Convergence
12m 52s
- Intro0:00
- Power Series0:09
- Definition0:19
- Radius & Interval of Convergence2:07
- Example 12:28
- Example 24:18
- Example 36:20
- Example 49:11
Taylor Series
15m 11s
- Intro0:00
- Taylor Series0:06
- MacLaurin Series0:45
- Example 11:02
- Example 22:45
- Example 36:04
- Example 48:23
- Example 511:49
Power Series Operations
16m 40s
- Intro0:00
- Operations0:07
- Example 1: Substitution1:05
- Example 2: Substitution3:41
- Example 3: Differentiation/ Integration5:39
- Example 4: Differentiation/ Integration9:55
- Example 5: Multiplying/ Dividing12:32
- Example 6: Multiplying/ Dividing14:50
Lagrange Error
7m 9s
- Intro0:00
- Power Series: Lagrange Error0:06
- Lagrange Remainder0:21
- Lagrange Error Bound0:50
- Example 11:06
- Example 23:27
Section 6: Practice Test
AP Calc BC Practice Test Section 1: Multi Choice Part 1
15m 45s
- Intro0:00
- Practice Problem 10:10
- Practice Problem 21:19
- Practice Problem 32:33
- Practice Problem 45:25
- Practice Problem 56:32
- Practice Problem 69:11
- Practice Problem 711:31
- Practice Problem 813:08
- Practice Problem 914:16
AP Calc BC Practice Test Section 1: Multi Choice Part 2
21m 38s
- Intro0:00
- Practice Problem 100:12
- Practice Problem 113:03
- Practice Problem 124:53
- Practice Problem 136:56
- Practice Problem 149:10
- Practice Problem 1512:17
- Practice Problem 1614:43
- Practice Problem 1716:18
- Practice Problem 1818:34
AP Calc BC Practice Test Section 1: Multi Choice Part 3
17m 31s
- Intro0:00
- Practice Problem 190:09
- Practice Problem 203:03
- Practice Problem 214:07
- Practice Problem 225:41
- Practice Problem 238:48
- Practice Problem 2411:16
- Practice Problem 2512:53
- Practice Problem 2614:12
- Practice Problem 2715:21
AP Calc BC Practice Test Section 1: Multi Choice Part 4
14m 17s
- Intro0:00
- Practice Problem 280:08
- Practice Problem 291:19
- Practice Problem 302:15
- Practice Problem 314:19
- Practice Problem 326:54
- Practice Problem 338:13
- Practice Problem 349:03
- Practice Problem 3510:21
- Practice Problem 3611:42
AP Calc BC Practice Test Section 1: Multi Choice Part 5
22m 45s
- Intro0:00
- Practice Problem 370:10
- Practice Problem 384:09
- Practice Problem 397:21
- Practice Problem 409:42
- Practice Problem 4111:35
- Practice Problem 4214:01
- Practice Problem 4315:50
- Practice Problem 4416:43
- Practice Problem 4519:35
AP Calc BC Practice Test Section 1: Free Response Part 1
9m 55s
- Intro0:00
- Practice Problem 1a0:08
- Practice Problem 1b1:30
- Practice Problem 1c3:08
- Practice Problem 2a3:50
- Practice Problem 2b5:40
- Practice Problem 2c7:24
AP Calc BC Practice Test Section 1: Free Response Part 2
10m 8s
- Intro0:00
- Practice Problem 3a0:09
- Practice Problem 3b3:01
- Practice Problem 4a3:55
- Practice Problem 4b5:43
AP Calc BC Practice Test Section 1: Free Response Part 3
13m 58s
- Intro0:00
- Practice Problem 5a0:07
- Practice Problem 5b2:21
- Practice Problem 5c4:21
- Practice Problem 6a6:16
- Practice Problem 6b8:57
- Practice Problem 6c11:03
Loading...
This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Calculus BC
For more information, please see full course syllabus of Calculus BC
Calculus BC Absolute Convergence
Lecture Description
In this lesson, our instructor John Zhu gives an introduction to absolute convergence. He talks about absolute convergence and looking at the series as an absolute value. He works out several example problems.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine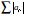 converges then
converges then 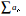 “absolutely converges”
“absolutely converges”




Start Learning Now
Our free lessons will get you started (Adobe Flash® required).
Sign up for Educator.comGet immediate access to our entire library.
Membership Overview