

Professor Murray
Sine and Cosine Functions
Slide Duration:Table of Contents
39m 5s
- Intro0:00
- Degrees0:22
- Circle is 360 Degrees0:48
- Splitting a Circle1:13
- Radians2:08
- Circle is 2 Pi Radians2:31
- One Radian2:52
- Half-Circle and Right Angle4:00
- Converting Between Degrees and Radians6:24
- Formulas for Degrees and Radians6:52
- Coterminal, Complementary, Supplementary Angles7:23
- Coterminal Angles7:30
- Complementary Angles9:40
- Supplementary Angles10:08
- Example 1: Dividing a Circle10:38
- Example 2: Converting Between Degrees and Radians11:56
- Example 3: Quadrants and Coterminal Angles14:18
- Extra Example 1: Common Angle Conversions-1
- Extra Example 2: Quadrants and Coterminal Angles-2
43m 16s
- Intro0:00
- Sine and Cosine0:15
- Unit Circle0:22
- Coordinates on Unit Circle1:03
- Right Triangles1:52
- Adjacent, Opposite, Hypotenuse2:25
- Master Right Triangle Formula: SOHCAHTOA2:48
- Odd Functions, Even Functions4:40
- Example: Odd Function4:56
- Example: Even Function7:30
- Example 1: Sine and Cosine10:27
- Example 2: Graphing Sine and Cosine Functions14:39
- Example 3: Right Triangle21:40
- Example 4: Odd, Even, or Neither26:01
- Extra Example 1: Right Triangle-1
- Extra Example 2: Graphing Sine and Cosine Functions-2
33m 5s
- Intro0:00
- 45-45-90 Triangle and 30-60-90 Triangle0:08
- 45-45-90 Triangle0:21
- 30-60-90 Triangle2:06
- Mnemonic: All Students Take Calculus (ASTC)5:21
- Using the Unit Circle5:59
- New Angles6:21
- Other Quadrants9:43
- Mnemonic: All Students Take Calculus10:13
- Example 1: Convert, Quadrant, Sine/Cosine13:11
- Example 2: Convert, Quadrant, Sine/Cosine16:48
- Example 3: All Angles and Quadrants20:21
- Extra Example 1: Convert, Quadrant, Sine/Cosine-1
- Extra Example 2: All Angles and Quadrants-2
52m 3s
- Intro0:00
- Amplitude and Period of a Sine Wave0:38
- Sine Wave Graph0:58
- Amplitude: Distance from Middle to Peak1:18
- Peak: Distance from Peak to Peak2:41
- Phase Shift and Vertical Shift4:13
- Phase Shift: Distance Shifted Horizontally4:16
- Vertical Shift: Distance Shifted Vertically6:48
- Example 1: Amplitude/Period/Phase and Vertical Shift8:04
- Example 2: Amplitude/Period/Phase and Vertical Shift17:39
- Example 3: Find Sine Wave Given Attributes25:23
- Extra Example 1: Amplitude/Period/Phase and Vertical Shift-1
- Extra Example 2: Find Cosine Wave Given Attributes-2
36m 4s
- Intro0:00
- Tangent and Cotangent Definitions0:21
- Tangent Definition0:25
- Cotangent Definition0:47
- Master Formula: SOHCAHTOA1:01
- Mnemonic1:16
- Tangent and Cotangent Values2:29
- Remember Common Values of Sine and Cosine2:46
- 90 Degrees Undefined4:36
- Slope and Menmonic: ASTC5:47
- Uses of Tangent5:54
- Example: Tangent of Angle is Slope6:09
- Sign of Tangent in Quadrants7:49
- Example 1: Graph Tangent and Cotangent Functions10:42
- Example 2: Tangent and Cotangent of Angles16:09
- Example 3: Odd, Even, or Neither18:56
- Extra Example 1: Tangent and Cotangent of Angles-1
- Extra Example 2: Tangent and Cotangent of Angles-2
27m 18s
- Intro0:00
- Secant and Cosecant Definitions0:17
- Secant Definition0:18
- Cosecant Definition0:33
- Example 1: Graph Secant Function0:48
- Example 2: Values of Secant and Cosecant6:49
- Example 3: Odd, Even, or Neither12:49
- Extra Example 1: Graph of Cosecant Function-1
- Extra Example 2: Values of Secant and Cosecant-2
32m 58s
- Intro0:00
- Arcsine Function0:24
- Restrictions between -1 and 10:43
- Arcsine Notation1:26
- Arccosine Function3:07
- Restrictions between -1 and 13:36
- Cosine Notation3:53
- Arctangent Function4:30
- Between -Pi/2 and Pi/24:44
- Tangent Notation5:02
- Example 1: Domain/Range/Graph of Arcsine5:45
- Example 2: Arcsin/Arccos/Arctan Values10:46
- Example 3: Domain/Range/Graph of Arctangent17:14
- Extra Example 1: Domain/Range/Graph of Arccosine-1
- Extra Example 2: Arcsin/Arccos/Arctan Values-2
31m 8s
- Intro0:00
- Inverse Trigonometric Function Domains and Ranges0:31
- Arcsine0:41
- Arccosine1:14
- Arctangent1:41
- Example 1: Arcsines of Common Values2:44
- Example 2: Odd, Even, or Neither5:57
- Example 3: Arccosines of Common Values12:24
- Extra Example 1: Arctangents of Common Values-1
- Extra Example 2: Arcsin/Arccos/Arctan Values-2
19m 11s
- Intro0:00
- Pythagorean Identity0:17
- Pythagorean Triangle0:27
- Pythagorean Identity0:45
- Example 1: Use Pythagorean Theorem to Prove Pythagorean Identity1:14
- Example 2: Find Angle Given Cosine and Quadrant4:18
- Example 3: Verify Trigonometric Identity8:00
- Extra Example 1: Use Pythagorean Identity to Prove Pythagorean Theorem-1
- Extra Example 2: Find Angle Given Cosine and Quadrant-2
23m 16s
- Intro0:00
- Main Formulas0:19
- Companion to Pythagorean Identity0:27
- For Cotangents and Cosecants0:52
- How to Remember0:58
- Example 1: Prove the Identity1:40
- Example 2: Given Tan Find Sec3:42
- Example 3: Prove the Identity7:45
- Extra Example 1: Prove the Identity-1
- Extra Example 2: Given Sec Find Tan-2
52m 52s
- Intro0:00
- Addition and Subtraction Formulas0:09
- How to Remember0:48
- Cofunction Identities1:31
- How to Remember Graphically1:44
- Where to Use Cofunction Identities2:52
- Example 1: Derive the Formula for cos(A-B)3:08
- Example 2: Use Addition and Subtraction Formulas16:03
- Example 3: Use Addition and Subtraction Formulas to Prove Identity25:11
- Extra Example 1: Use cos(A-B) and Cofunction Identities-1
- Extra Example 2: Convert to Radians and use Formulas-2
29m 5s
- Intro0:00
- Main Formula0:07
- How to Remember from Addition Formula0:18
- Two Other Forms1:35
- Example 1: Find Sine and Cosine of Angle using Double Angle3:16
- Example 2: Prove Trigonometric Identity using Double Angle9:37
- Example 3: Use Addition and Subtraction Formulas12:38
- Extra Example 1: Find Sine and Cosine of Angle using Double Angle-1
- Extra Example 2: Prove Trigonometric Identity using Double Angle-2
43m 55s
- Intro0:00
- Main Formulas0:09
- Confusing Part0:34
- Example 1: Find Sine and Cosine of Angle using Half-Angle0:54
- Example 2: Prove Trigonometric Identity using Half-Angle11:51
- Example 3: Prove the Half-Angle Formula for Tangents18:39
- Extra Example 1: Find Sine and Cosine of Angle using Half-Angle-1
- Extra Example 2: Prove Trigonometric Identity using Half-Angle-2
25m 43s
- Intro0:00
- Master Formula for Right Angles0:11
- SOHCAHTOA0:15
- Only for Right Triangles1:26
- Example 1: Find All Angles in a Triangle2:19
- Example 2: Find Lengths of All Sides of Triangle7:39
- Example 3: Find All Angles in a Triangle11:00
- Extra Example 1: Find All Angles in a Triangle-1
- Extra Example 2: Find Lengths of All Sides of Triangle-2
56m 40s
- Intro0:00
- Law of Sines Formula0:18
- SOHCAHTOA0:27
- Any Triangle0:59
- Graphical Representation1:25
- Solving Triangle Completely2:37
- When to Use Law of Sines2:55
- ASA, SAA, SSA, AAA2:59
- SAS, SSS for Law of Cosines7:11
- Example 1: How Many Triangles Satisfy Conditions, Solve Completely8:44
- Example 2: How Many Triangles Satisfy Conditions, Solve Completely15:30
- Example 3: How Many Triangles Satisfy Conditions, Solve Completely28:32
- Extra Example 1: How Many Triangles Satisfy Conditions, Solve Completely-1
- Extra Example 2: How Many Triangles Satisfy Conditions, Solve Completely-2
49m 5s
- Intro0:00
- Law of Cosines Formula0:23
- Graphical Representation0:34
- Relates Sides to Angles1:00
- Any Triangle1:20
- Generalization of Pythagorean Theorem1:32
- When to Use Law of Cosines2:26
- SAS, SSS2:30
- Heron's Formula4:49
- Semiperimeter S5:11
- Example 1: How Many Triangles Satisfy Conditions, Solve Completely5:53
- Example 2: How Many Triangles Satisfy Conditions, Solve Completely15:19
- Example 3: Find Area of a Triangle Given All Side Lengths26:33
- Extra Example 1: How Many Triangles Satisfy Conditions, Solve Completely-1
- Extra Example 2: Length of Third Side and Area of Triangle-2
27m 37s
- Intro0:00
- Master Right Triangle Formula and Law of Cosines0:19
- SOHCAHTOA0:27
- Law of Cosines1:23
- Heron's Formula2:22
- Semiperimeter S2:37
- Example 1: Area of Triangle with Two Sides and One Angle3:12
- Example 2: Area of Triangle with Three Sides6:11
- Example 3: Area of Triangle with Three Sides, No Heron's Formula8:50
- Extra Example 1: Area of Triangle with Two Sides and One Angle-1
- Extra Example 2: Area of Triangle with Two Sides and One Angle-2
34m 25s
- Intro0:00
- Formulas to Remember0:11
- SOHCAHTOA0:15
- Law of Sines0:55
- Law of Cosines1:48
- Heron's Formula2:46
- Example 1: Telephone Pole Height4:01
- Example 2: Bridge Length7:48
- Example 3: Area of Triangular Field14:20
- Extra Example 1: Kite Height-1
- Extra Example 2: Roads to a Town-2
46m 42s
- Intro0:00
- Vector Formulas and Concepts0:12
- Vectors as Arrows0:28
- Magnitude0:38
- Direction0:50
- Drawing Vectors1:16
- Uses of Vectors: Velocity, Force1:37
- Vector Magnitude Formula3:15
- Vector Direction Formula3:28
- Vector Components6:27
- Example 1: Magnitude and Direction of Vector8:00
- Example 2: Force to a Box on a Ramp12:25
- Example 3: Plane with Wind18:30
- Extra Example 1: Components of a Vector-1
- Extra Example 2: Ship with a Current-2
1h 7m 35s
- Intro0:00
- Polar Coordinates vs Rectangular/Cartesian Coordinates0:12
- Rectangular Coordinates, Cartesian Coordinates0:23
- Polar Coordinates0:59
- Converting Between Polar and Rectangular Coordinates2:06
- R2:16
- Theta2:48
- Example 1: Convert Rectangular to Polar Coordinates6:53
- Example 2: Convert Polar to Rectangular Coordinates17:28
- Example 3: Graph the Polar Equation28:00
- Extra Example 1: Convert Polar to Rectangular Coordinates-1
- Extra Example 2: Graph the Polar Equation-2
35m 59s
- Intro0:00
- Main Definition0:07
- Number i0:23
- Complex Number Form0:33
- Powers of Imaginary Number i1:00
- Repeating Pattern1:43
- Operations on Complex Numbers3:30
- Adding and Subtracting Complex Numbers3:39
- Multiplying Complex Numbers4:39
- FOIL Method5:06
- Conjugation6:29
- Dividing Complex Numbers7:34
- Conjugate of Denominator7:45
- Example 1: Solve For Complex Number z11:02
- Example 2: Expand and Simplify15:34
- Example 3: Simplify the Powers of i17:50
- Extra Example 1: Simplify-1
- Extra Example 2: All Complex Numbers Satisfying Equation-2
40m 43s
- Intro0:00
- Polar Coordinates0:49
- Rectangular Form0:52
- Polar Form1:25
- R and Theta1:51
- Polar Form Conversion2:27
- R and Theta2:35
- Optimal Values4:05
- Euler's Formula4:25
- Multiplying Two Complex Numbers in Polar Form6:10
- Multiply r's Together and Add Exponents6:32
- Example 1: Convert Rectangular to Polar Form7:17
- Example 2: Convert Polar to Rectangular Form13:49
- Example 3: Multiply Two Complex Numbers17:28
- Extra Example 1: Convert Between Rectangular and Polar Forms-1
- Extra Example 2: Simplify Expression to Polar Form-2
57m 37s
- Intro0:00
- Introduction to DeMoivre's Theorem0:10
- n nth Roots3:06
- DeMoivre's Theorem: Finding nth Roots3:52
- Relation to Unit Circle6:29
- One nth Root for Each Value of k7:11
- Example 1: Convert to Polar Form and Use DeMoivre's Theorem8:24
- Example 2: Find Complex Eighth Roots15:27
- Example 3: Find Complex Roots27:49
- Extra Example 1: Convert to Polar Form and Use DeMoivre's Theorem-1
- Extra Example 2: Find Complex Fourth Roots-2
For more information, please see full course syllabus of Trigonometry
Trigonometry Sine and Cosine Functions
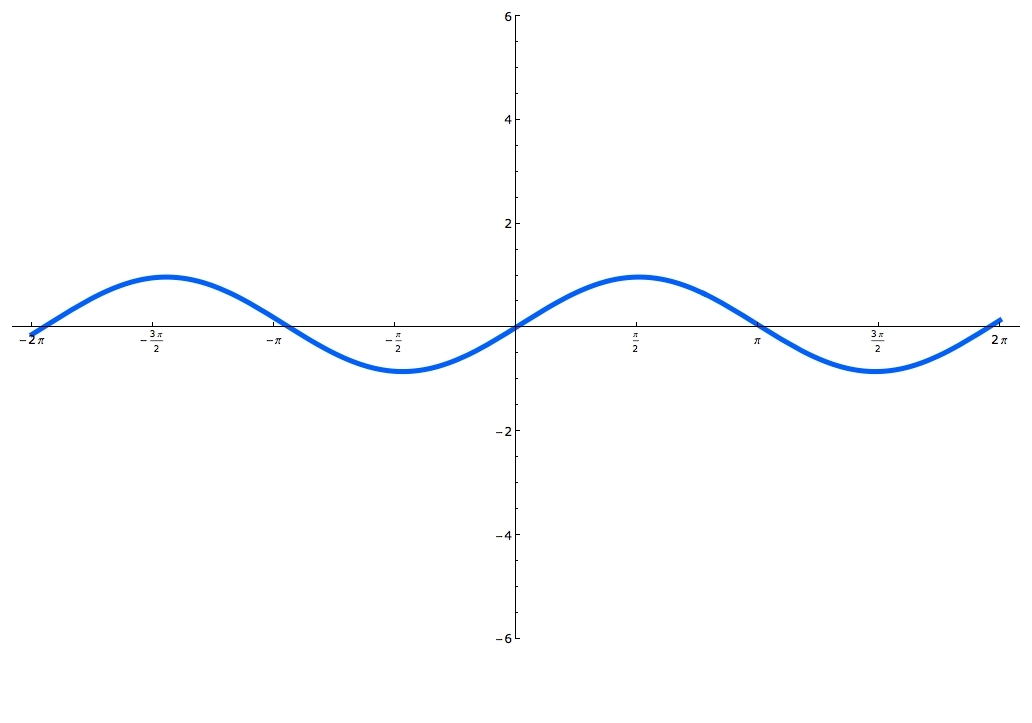
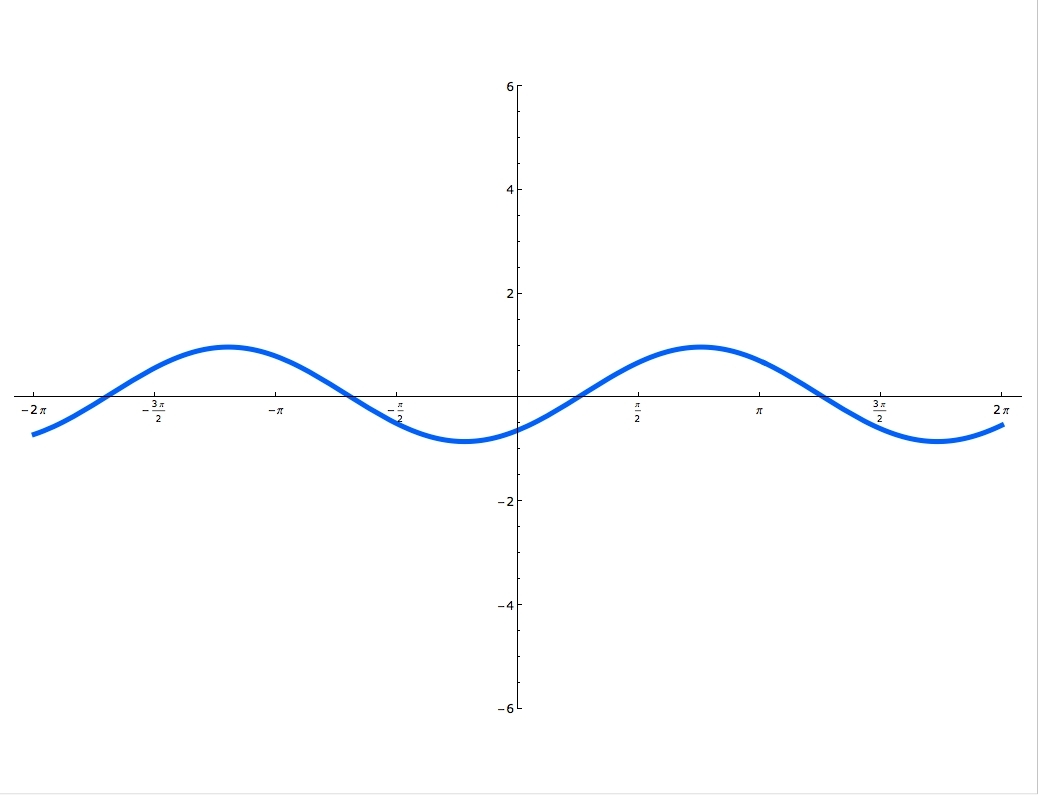
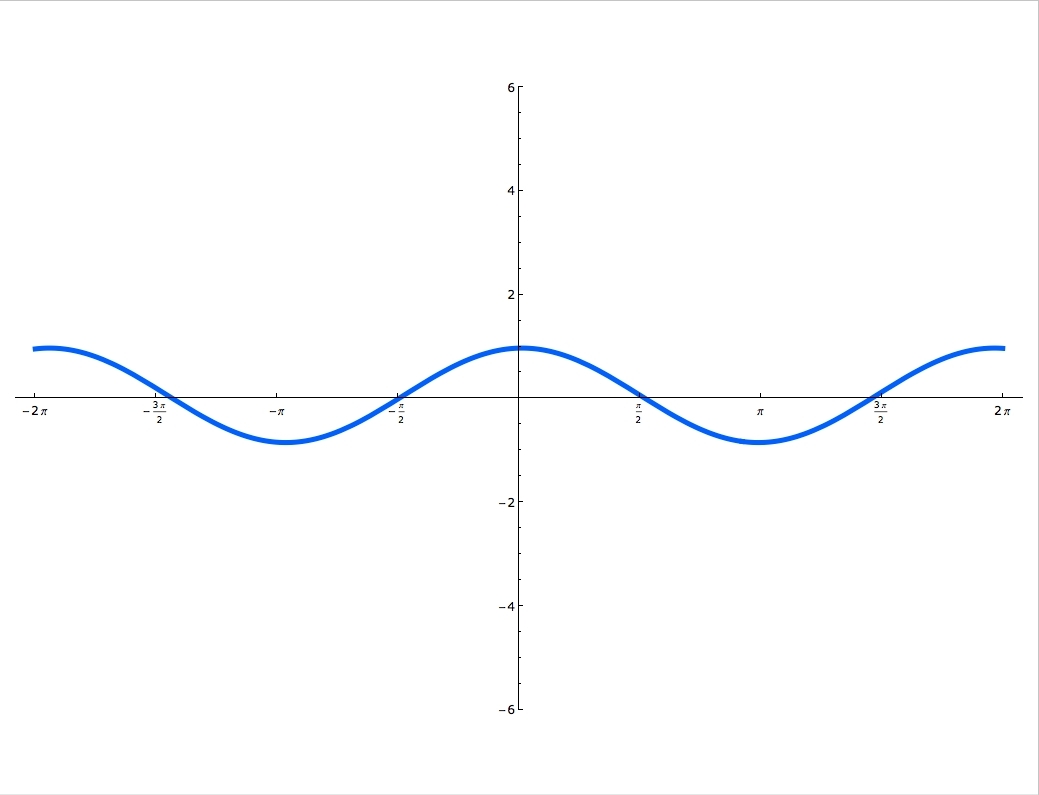
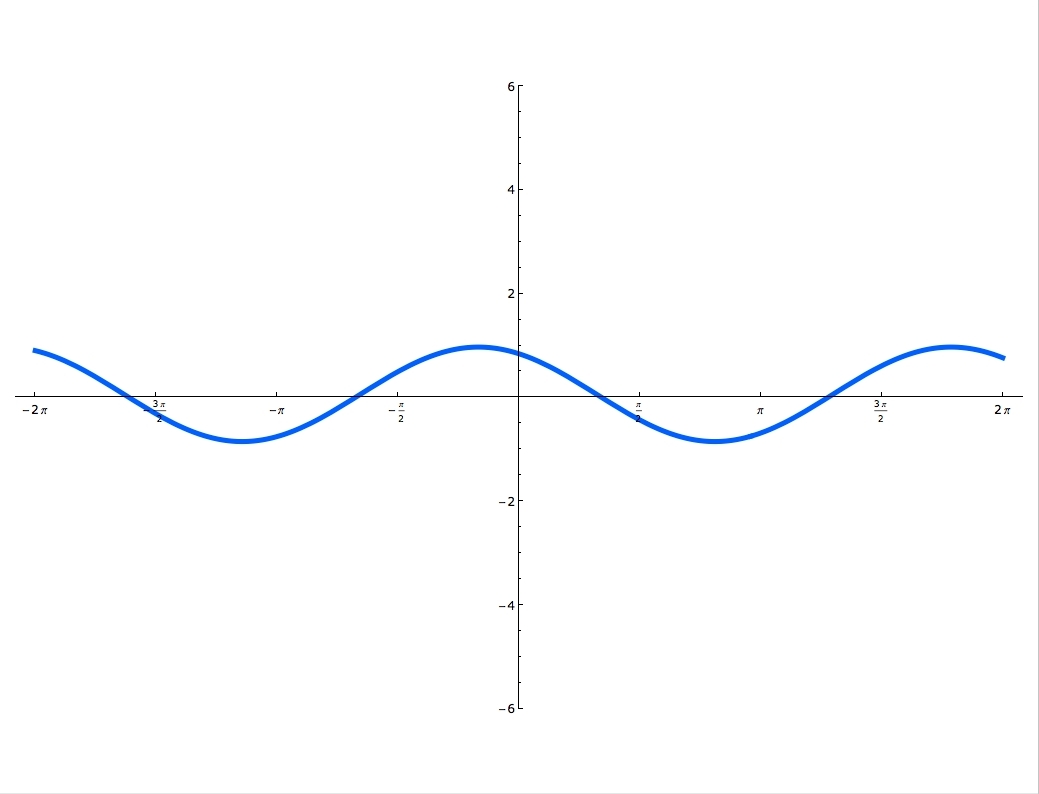
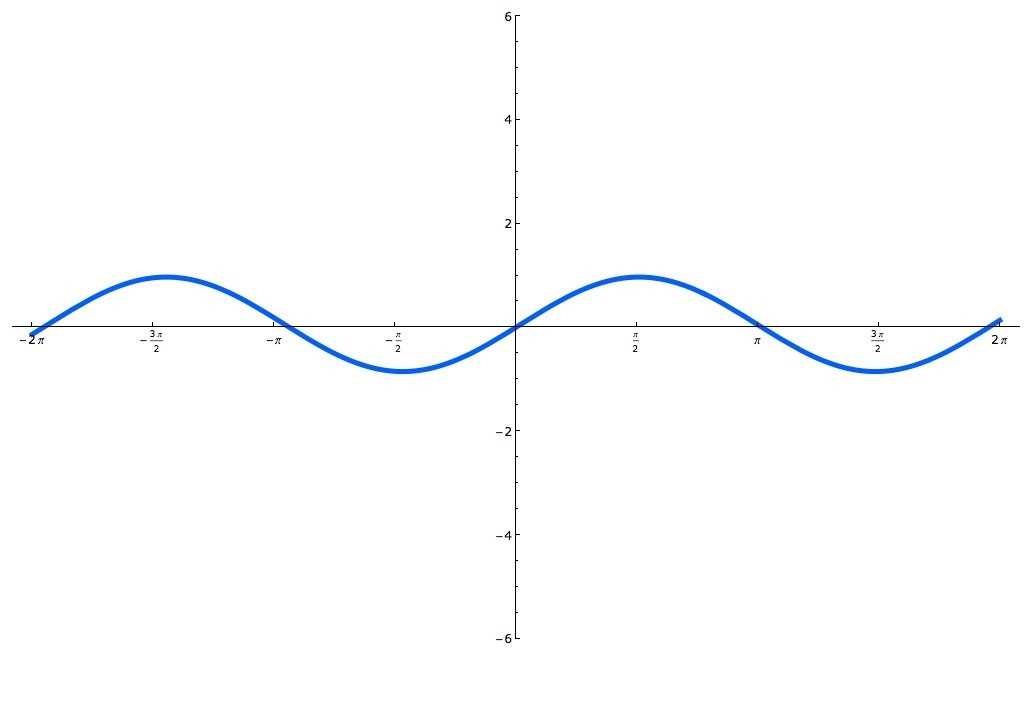
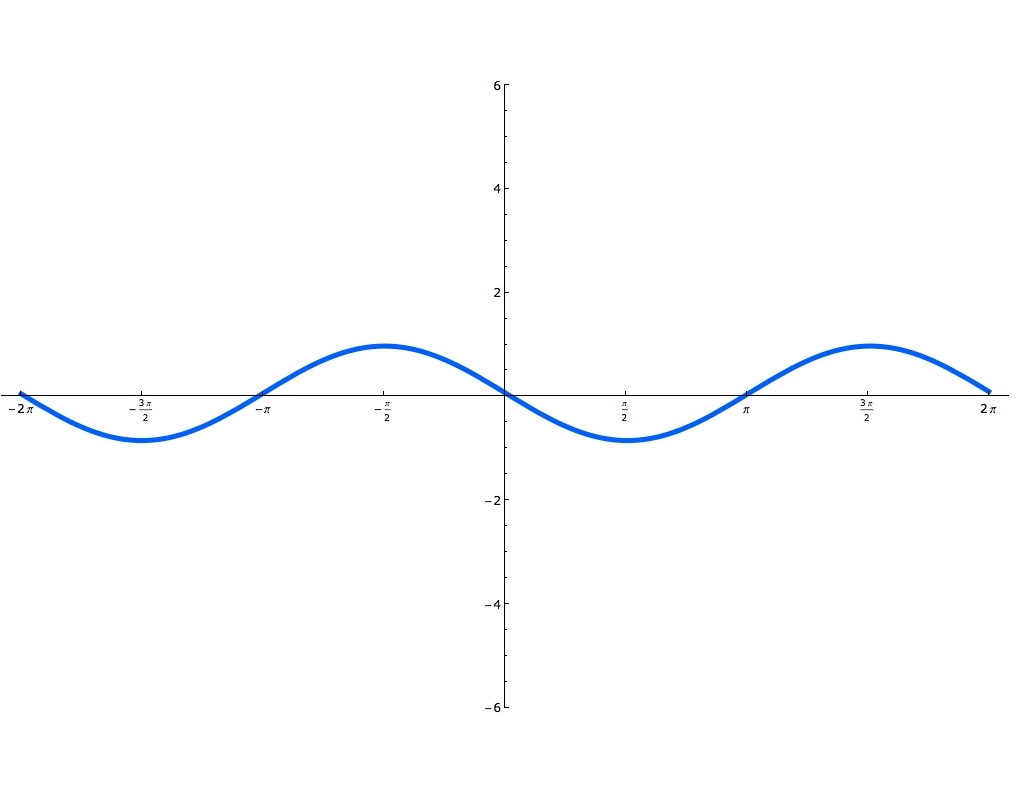
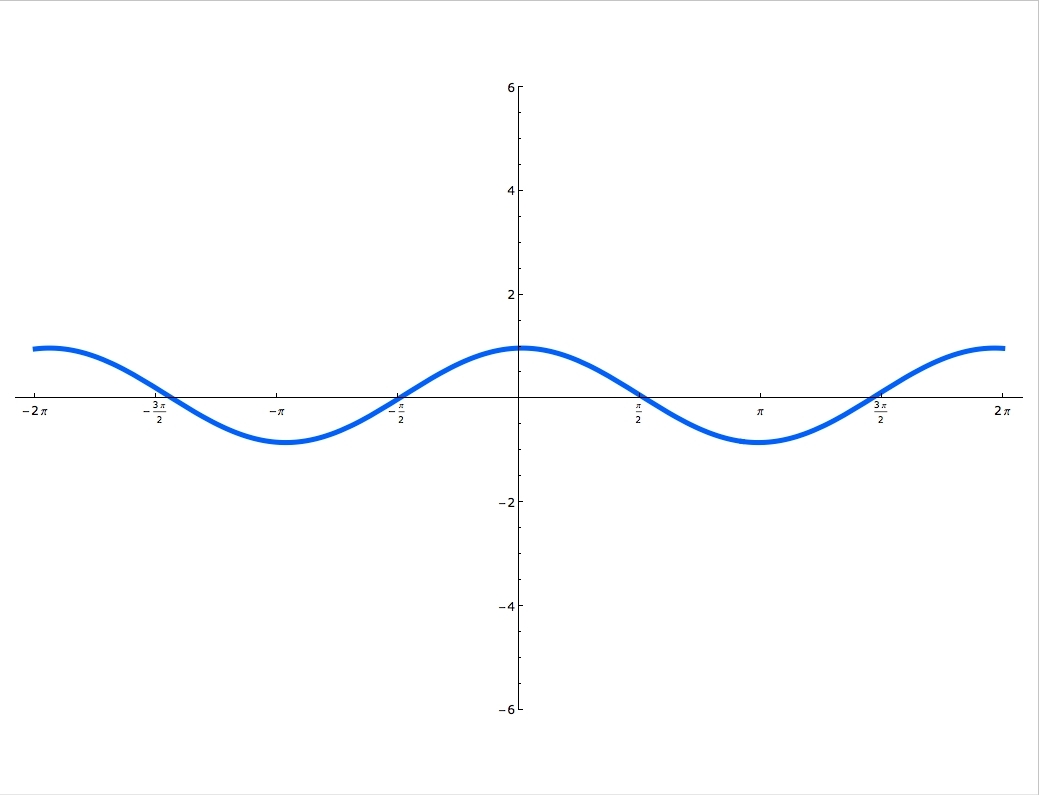
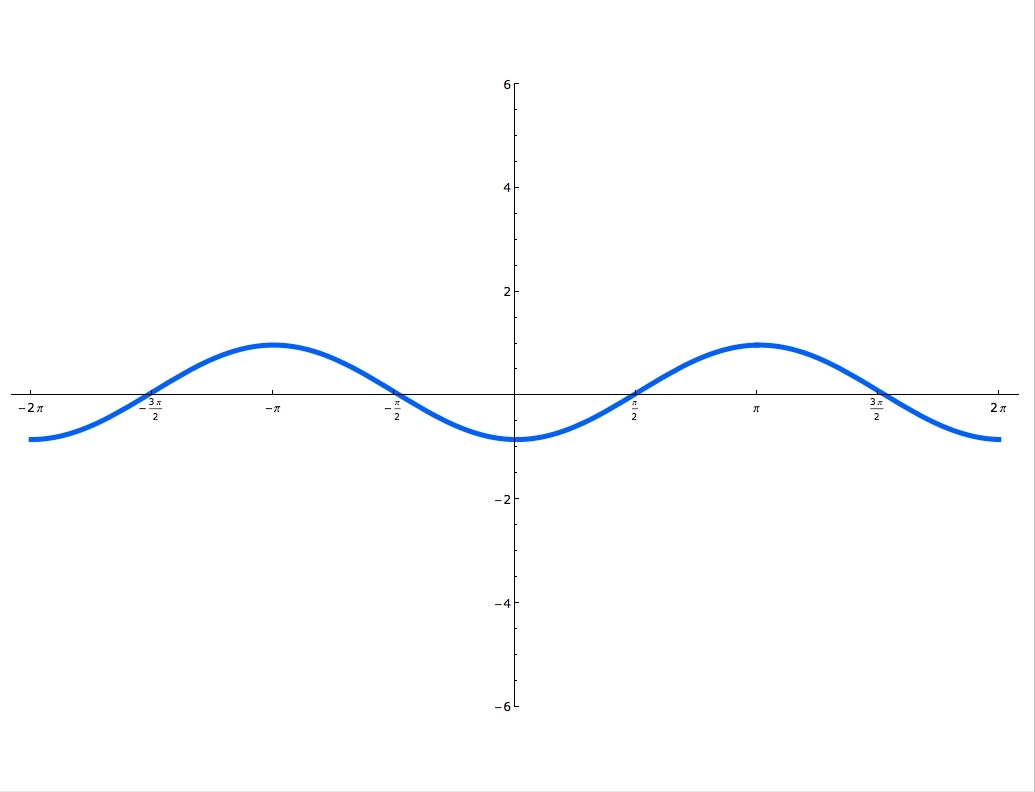
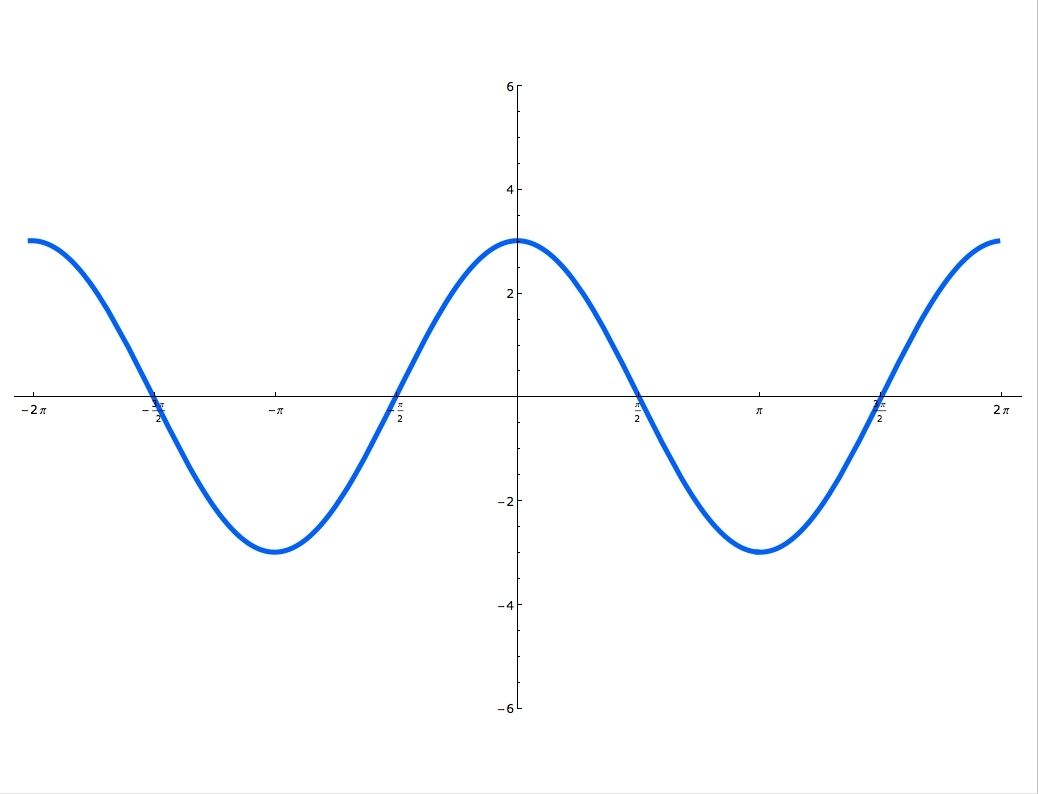
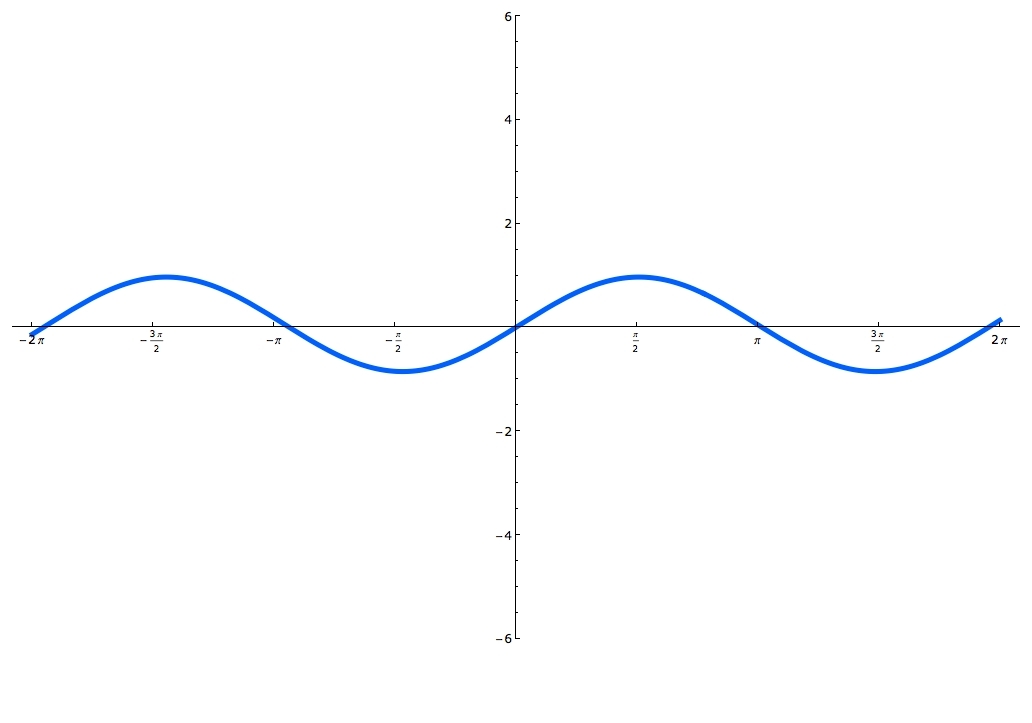
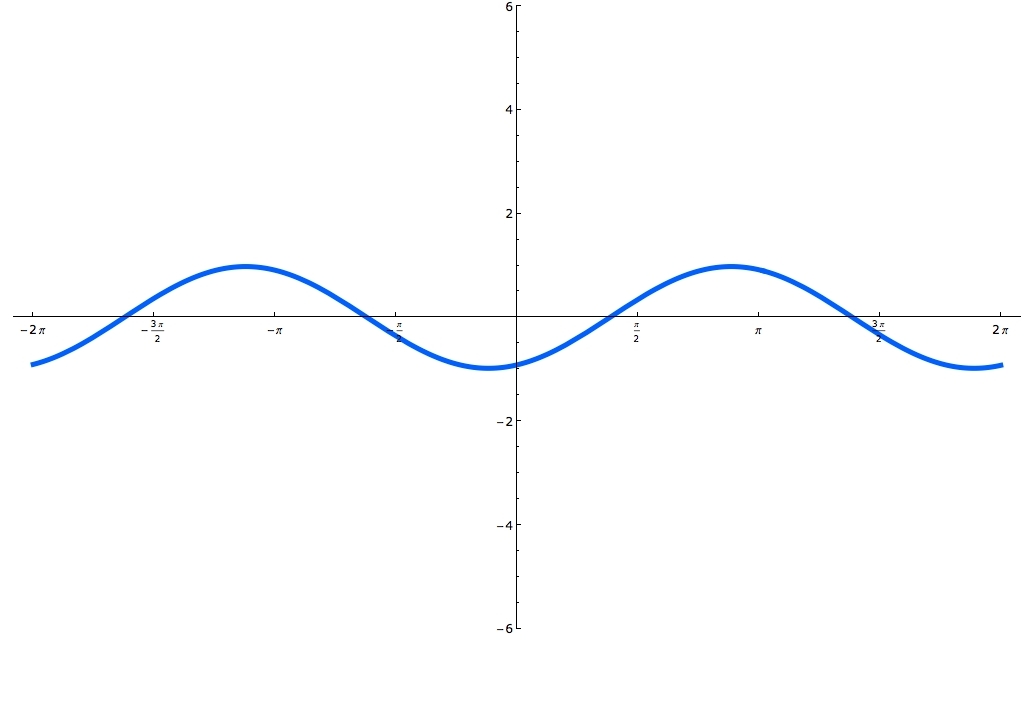
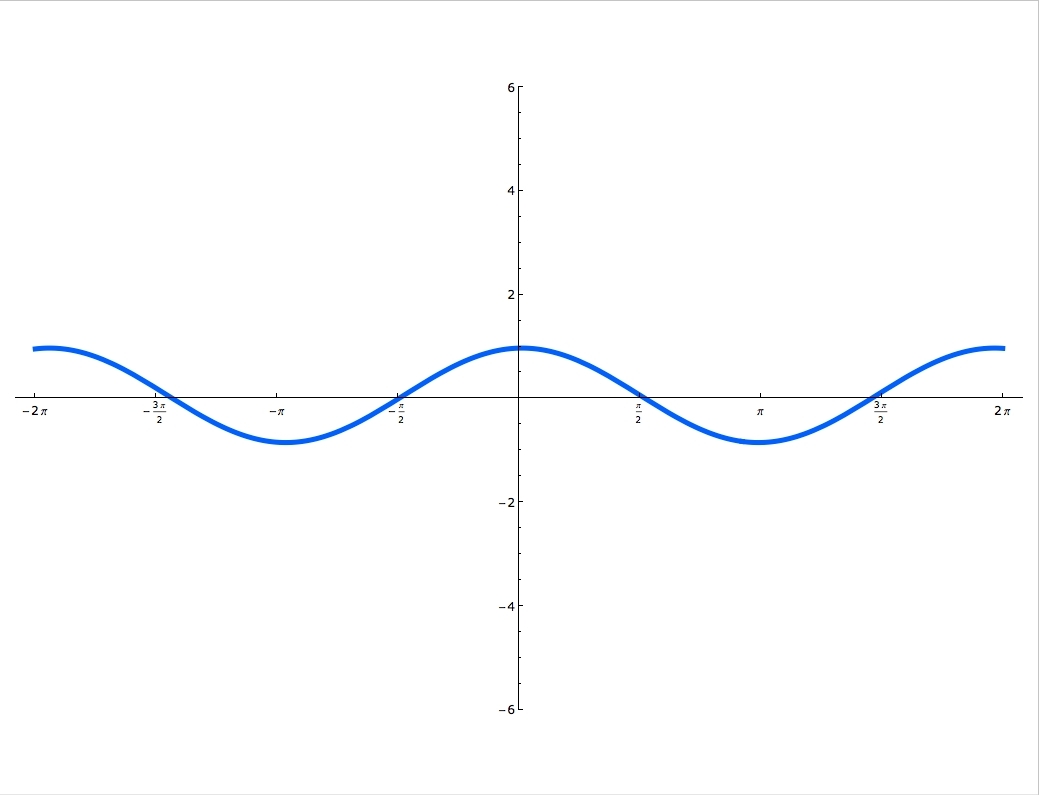
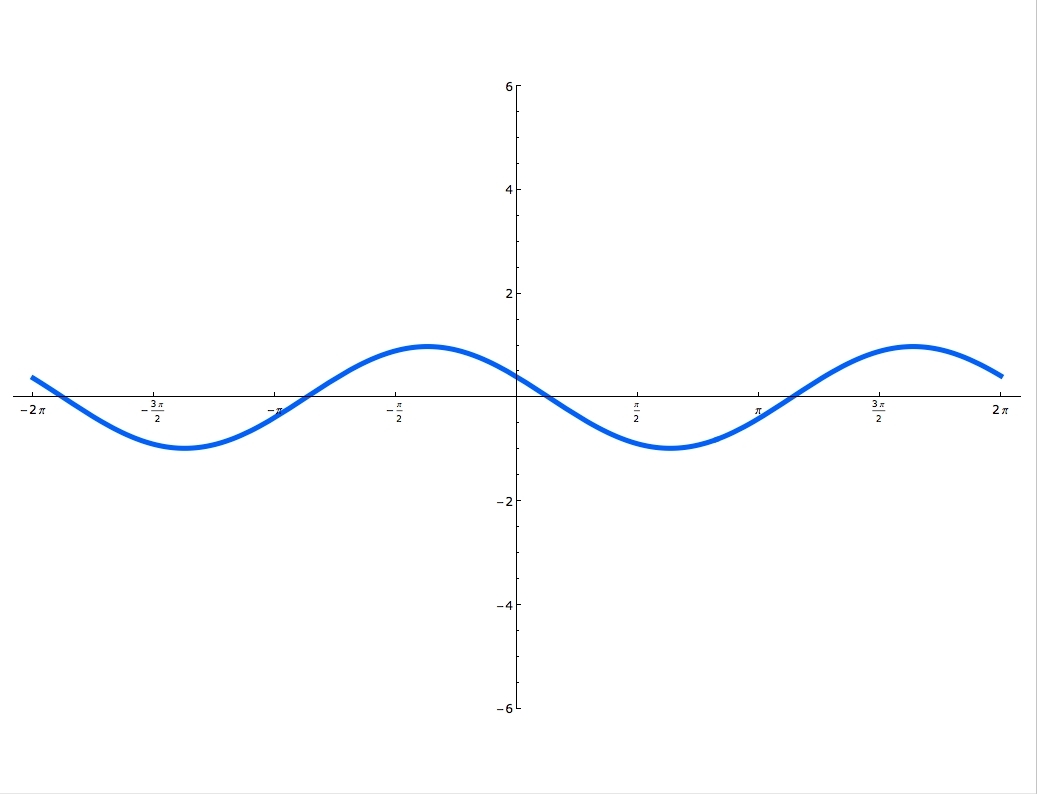
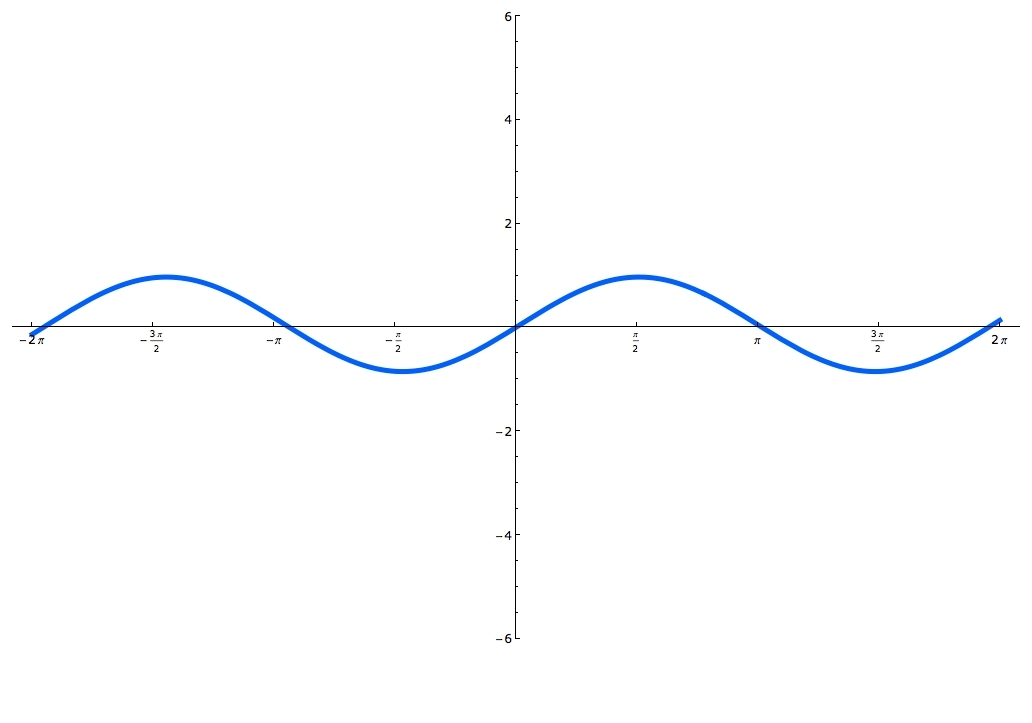
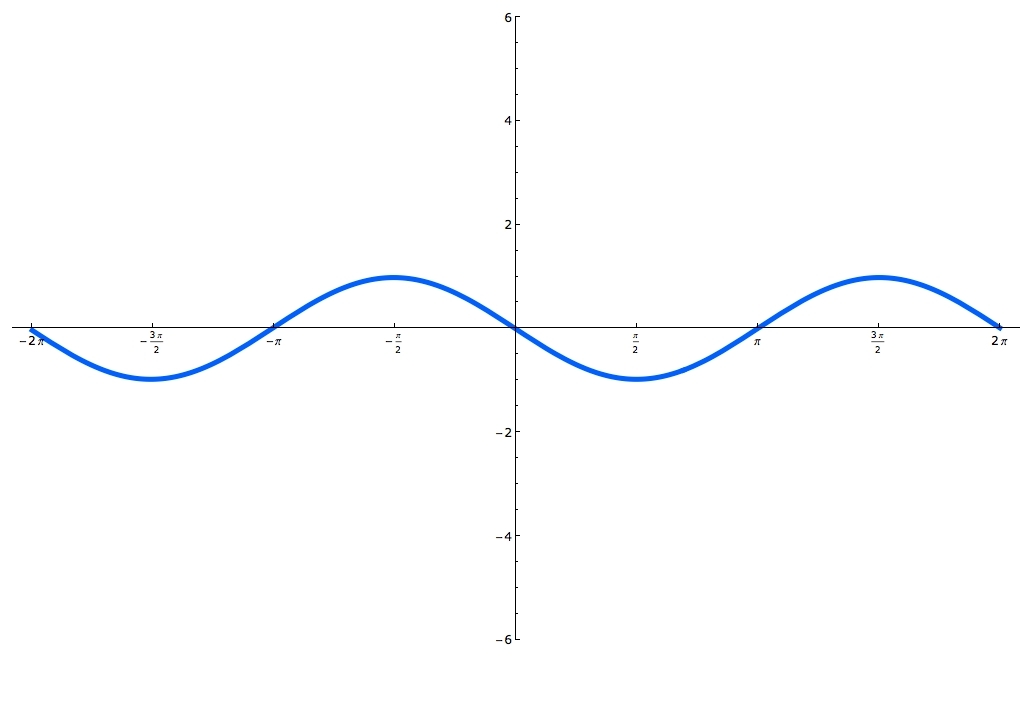
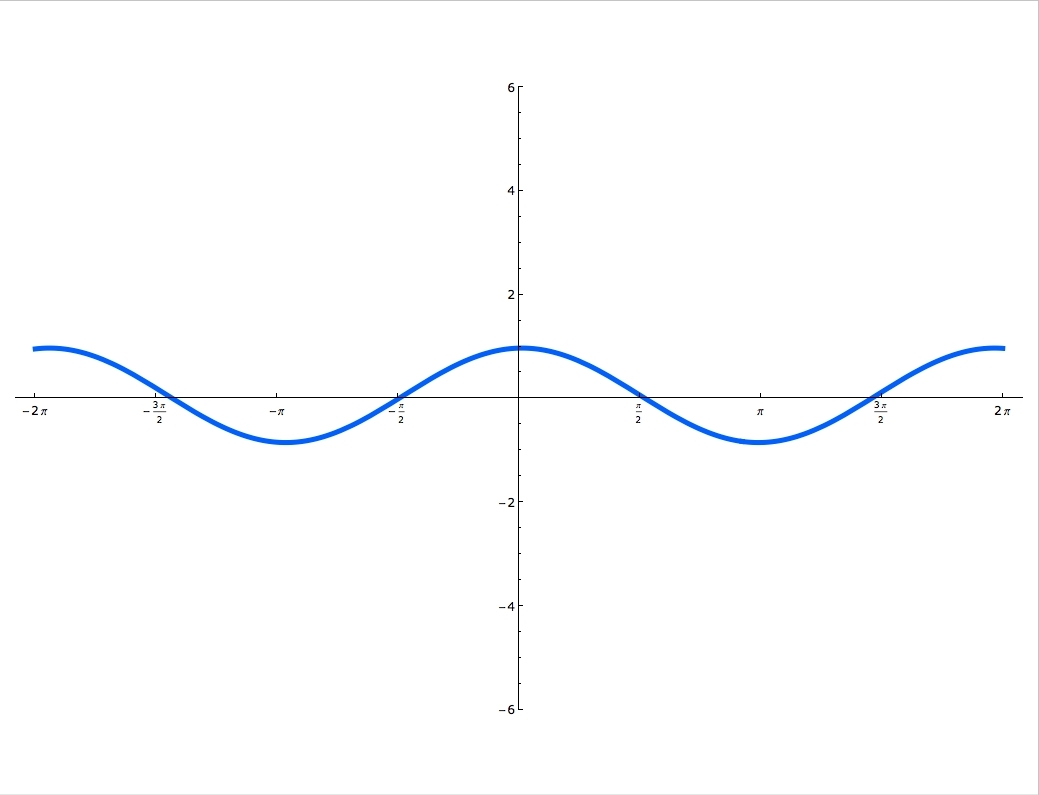
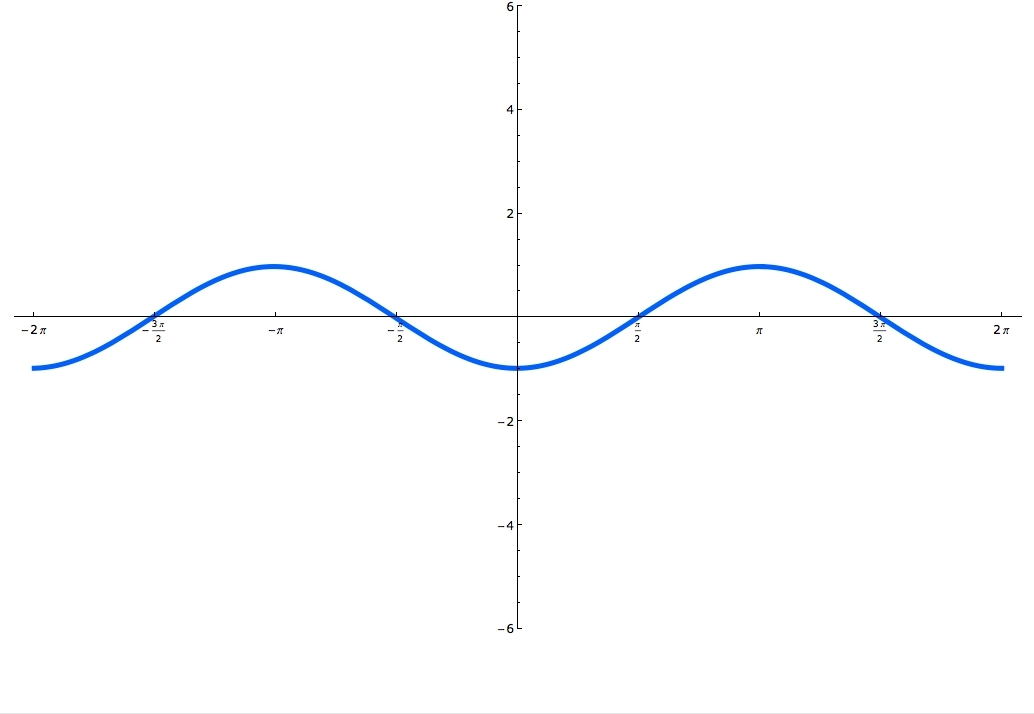
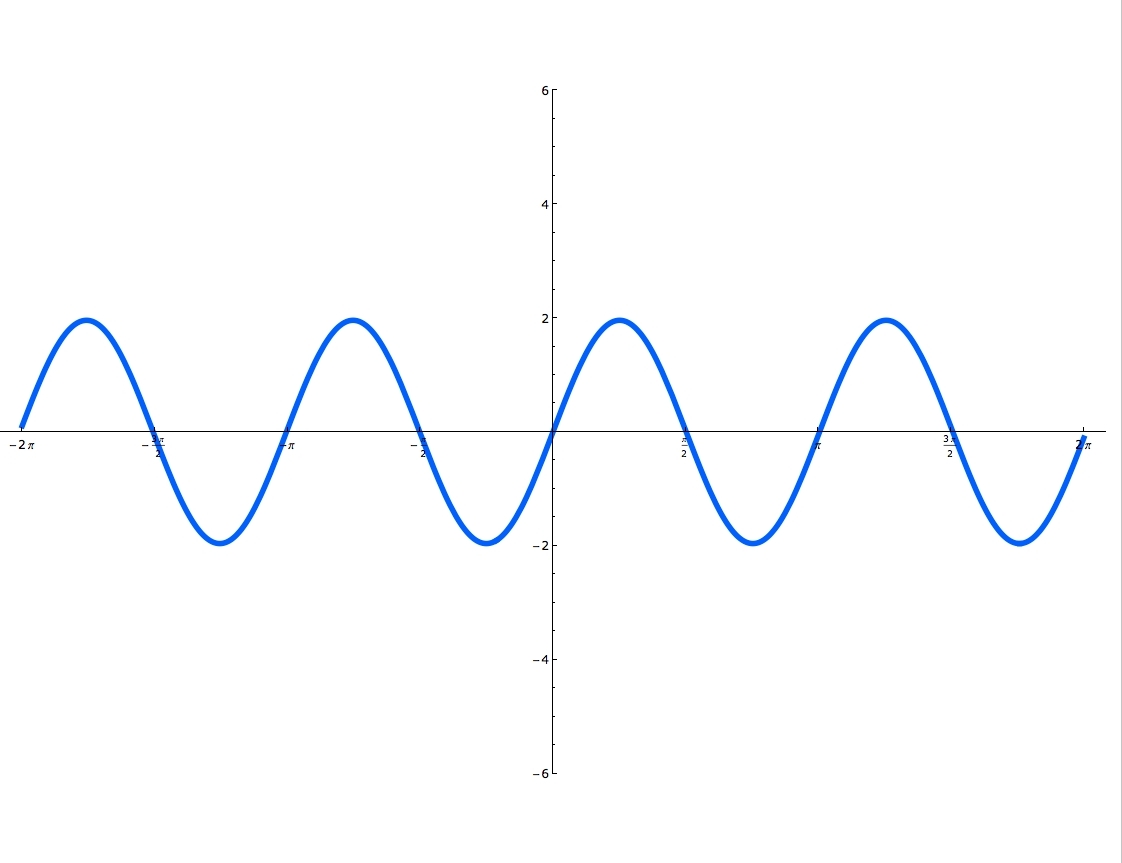
Sine and cosine functions are mostly used in terms of right triangles. There are special formulas on how to use them and you can master these formulas, by using the Sohcahtoa. Understanding what a Unit Circle is will help clarify where the sine and cosine functions are. Unit Circle is a circle with a radius of one. When you draw an angle θ in a standard position (starting on the positive x-axis), the coordinates of its terminal side on the unit circle are the cosine and the sine of θ. The x-coordinate is cosine and the y-coordinate is sine. In this lecture you'll learn when the function is odd and when it's even and you'll also practice graphing sine and cosine functions.
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
- - Allow users to view the embedded video in full-size.










































 Answer Engine
Answer Engine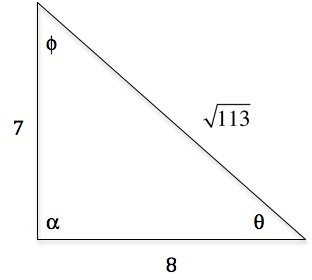




0 answers
Post by Tom Mei on June 21 at 03:08:00 AM
1 answer
Mon Jun 15, 2020 10:24 AM
Post by Victoria Su on June 13, 2020
Hi
For example 4, I understand why they odd/even based on the graph. However, I am not too sure how it works with plugging in the x values for f(x ) or g(x). I tried plugging them in but didn't get the correct answer.
1 answer
Fri Apr 3, 2020 10:03 AM
Post by Cheung Chun Hei on April 1, 2020
I still don't get the part about whether the graph is rotational or mirror symmetry and whether it is odd or even. Can you explain this a bit and thank you so much!
1 answer
Fri Mar 27, 2020 9:55 AM
Post by Yanping Du on March 25, 2020
What happens when a graph is both mirror symmetric and rotationally symmetric? Is that possible?
1 answer
Sun Mar 8, 2020 10:58 AM
Post by susiexuthus on March 7, 2020
When I try to load the extra examples, it says in the bottom right corner "audio source file does not exist". Is it just my computer?
1 answer
Wed Apr 17, 2019 1:35 PM
Post by Christopher Wang on April 16, 2019
I don't understand how you derived the fact that cos pi is -1 and sin pi is 0.
1 answer
Tue Jun 7, 2016 12:31 PM
Post by Bassam Razzaq on June 5, 2016
In example 2, how can the graph has value of x-coordinate more than 2pi. I thought 2pi was the last point as also seen in unit circle.
1 answer
Mon Nov 2, 2015 2:18 PM
Post by Peter Ke on October 30, 2015
In example 4, I DON'T get how g(x) is odd. I thought it was even.
3 answers
Wed Nov 11, 2015 9:23 AM
Post by Peter Ke on October 30, 2015
For example 3 shouldn't Sin = 4/5 be 3/5? Because 3 is the opposite and 4 is adjacent.
1 answer
Thu Feb 19, 2015 3:36 PM
Post by patrick guerin on February 17, 2015
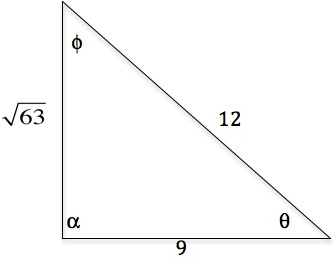
On practice question 2 it said the sin of theta was sqroot of 63 over 12 when i thought it was 9 over 12. Could you check it out please. Thanks.
1 answer
Fri Dec 19, 2014 9:31 AM
Post by katrina williams on December 17, 2014
In the second to last practice problem what amount does n represent? I was able to draw the original graph but got lost by how far to move it over.
1 answer
Mon Aug 4, 2014 7:48 PM
Post by patrick guerin on July 16, 2014
You placed a theta in the triangle that you created when you were defining sine cosine. Could you give me a small explanation on what theta is?
1 answer
Tue Jun 17, 2014 12:08 PM
Post by Austin Cunningham on June 9, 2014
How come at around 8:00, he says that x^2 is the same thing as f(x)?
3 answers
Thu Jun 5, 2014 11:43 AM
Post by Govind Balaji Srinivasa Raghavan on May 29, 2014
I dont know why. But all videos pause after sometime. Then it restarts again instead of continue. Also I cant skip to other part of video. Suppose tonight I watch half of video and go to sleep. Tomorrow morning, I have to watch from first, if i click on the play-head from where I should see, It automatically restarts.
1 answer
Tue Mar 4, 2014 5:00 PM
Post by Damien O Byrne on February 28, 2014
Does sin cos and tan formulas only apply to right angled triangles
1 answer
Wed Jan 22, 2014 3:04 PM
Post by Carroll Fields on January 16, 2014
In extra example I, at 3:30, why is the 'sine, cosine, and tangent of the right angle (alpha) , 1,0 , and undefined?And why for sine is it sin pi/2 ?
1 answer
Mon Oct 21, 2013 7:15 PM
Post by yannick Haberkorn on October 12, 2013
i have to congratulate you Dr.william murray because i actually really feel i am in a learning environment and it feels great . Much thanks
1 answer
Tue Apr 16, 2013 8:35 PM
Post by Dr. William Murray on January 27, 2013
Hi Emily,
Good question. As Jacob says in his post above, it's because we know that the graph of f(x-c) is like the graph of f(x), but shifted c units to the right. But you have to have the negative sign in there for this to work, so when we have f(x+(something)), we write it as f(x-(-something)). Then it's clear that the shift is (-something) units to the right, that is, (something) units to the left.
It's also worth reading Jacob's answer above -- same basic idea, but sometimes having a different person's phrasing helps.
Thanks for taking trigonometry!
Will Murray
1 answer
Tue Apr 16, 2013 8:34 PM
Post by Emily Engle on January 27, 2013
At 28:10 Why do you change Sin (x+ Pi/2) to Sin (x-(- Pi/2)) ?
1 answer
Fri Aug 31, 2012 5:45 PM
Post by Andraa Cram on June 25, 2012
@ 21:18, why, when going in the negative direction while graphing for sine (in red), does he draw the graph as (-Pi/2,-1) instead of (-Pi/2,1)? I'm very confused by this.
1 answer
Sun Jan 27, 2013 4:18 PM
Post by Lourdes Johnson on June 3, 2012
Why does the lecture restart around a quarter in?
1 answer
Sun Jan 27, 2013 4:16 PM
Post by Callistus Elue on May 23, 2012
the lecture reverts to the beginning almost as soon as it starts
1 answer
Sun Jan 27, 2013 4:12 PM
Post by Jacob Burley on April 25, 2011
At 26:33 Professor Murray gave the algebraic equation for a graph that has a constant which was f(x-c). Our equation sin(x+pi/2) has a positive where the negative is in the original equation. In order to get the correct sign there we must change the + sign into two - signs because two negatives make a positive.
I know I'm not the greatest at explaining things but hopefully this helps a little bit.
1 answer
Sun Jan 27, 2013 4:10 PM
Post by Shannon Bryington on February 28, 2011
At 27:40 on the video: Why was x + pi over 2 changed to x - neg pi over 2?
1 answer
Sun Jan 27, 2013 3:59 PM
Post by Santhini Dheenathayalan on January 19, 2011
Great!