

Professor Murray
Taylor Series and Maclaurin Series
Slide Duration:Table of Contents
24m 52s
- Intro0:00
- Important Equation0:07
- Where It Comes From (Product Rule)0:20
- Why Use It?0:35
- Lecture Example 11:24
- Lecture Example 23:30
- Shortcut: Tabular Integration7:34
- Example7:52
- Lecture Example 310:00
- Mnemonic: LIATE14:44
- Ln, Inverse, Algebra, Trigonometry, e15:38
- Additional Example 4-1
- Additional Example 5-2
25m 30s
- Intro0:00
- Important Equation0:07
- Powers (Odd and Even)0:19
- What To Do1:03
- Lecture Example 11:37
- Lecture Example 23:12
- Half-Angle Formulas6:16
- Both Powers Even6:31
- Lecture Example 37:06
- Lecture Example 410:59
- Additional Example 5-1
- Additional Example 6-2
30m 9s
- Intro0:00
- Important Equations0:06
- How They Work0:35
- Example1:45
- Remember: du and dx2:50
- Lecture Example 13:43
- Lecture Example 210:01
- Lecture Example 312:04
- Additional Example 4-1
- Additional Example 5-2
41m 22s
- Intro0:00
- Overview0:07
- Why Use It?0:18
- Lecture Example 11:21
- Lecture Example 26:52
- Lecture Example 313:28
- Additional Example 4-1
- Additional Example 5-2
20m
- Intro0:00
- Using Tables0:09
- Match Exactly0:32
- Lecture Example 11:16
- Lecture Example 25:28
- Lecture Example 38:51
- Additional Example 4-1
- Additional Example 5-2
22m 36s
- Intro0:00
- Trapezoidal Rule0:13
- Graphical Representation0:20
- How They Work1:08
- Formula1:47
- Why a Trapezoid?2:53
- Lecture Example 15:10
- Midpoint Rule8:23
- Why Midpoints?8:56
- Formula9:37
- Lecture Example 211:22
- Left/Right Endpoint Rule13:54
- Left Endpoint14:08
- Right Endpoint14:39
- Lecture Example 315:32
- Additional Example 4-1
- Additional Example 5-2
21m 8s
- Intro0:00
- Important Equation0:03
- Estimating Area0:28
- Difference from Previous Methods0:50
- General Principle1:09
- Lecture Example 13:49
- Lecture Example 26:32
- Lecture Example 39:07
- Additional Example 4-1
- Additional Example 5-2
44m 18s
- Intro0:00
- Horizontal and Vertical Asymptotes0:04
- Example: Horizontal0:16
- Formal Notation0:37
- Example: Vertical1:58
- Formal Notation2:29
- Lecture Example 15:01
- Lecture Example 27:41
- Lecture Example 311:32
- Lecture Example 415:49
- Formulas to Remember18:26
- Improper Integrals18:36
- Lecture Example 521:34
- Lecture Example 6 (Hidden Discontinuities)26:51
- Additional Example 7-1
- Additional Example 8-2
23m 20s
- Intro0:00
- Important Equation0:04
- Why It Works0:49
- Common Mistake1:21
- Lecture Example 12:14
- Lecture Example 26:26
- Lecture Example 310:49
- Additional Example 4-1
- Additional Example 5-2
28m 53s
- Intro0:00
- Important Equation0:05
- Surface Area0:38
- Relation to Arclength1:11
- Lecture Example 11:46
- Lecture Example 24:29
- Lecture Example 39:34
- Additional Example 4-1
- Additional Example 5-2
24m 37s
- Intro0:00
- Important Equation0:09
- Main Idea0:12
- Different Forces0:45
- Weight Density Constant1:10
- Variables (Depth and Width)2:21
- Lecture Example 13:28
- Additional Example 2-1
- Additional Example 3-2
25m 39s
- Intro0:00
- Important Equation0:07
- Main Idea0:25
- Centroid1:00
- Area1:28
- Lecture Example 11:44
- Lecture Example 26:13
- Lecture Example 310:04
- Additional Example 4-1
- Additional Example 5-2
22m 26s
- Intro0:00
- Important Equations0:05
- Slope of Tangent Line0:30
- Arc length1:03
- Lecture Example 11:40
- Lecture Example 24:23
- Lecture Example 38:38
- Additional Example 4-1
- Additional Example 5-2
30m 59s
- Intro0:00
- Important Equations0:05
- Polar Coordinates in Calculus0:42
- Area0:58
- Arc length1:41
- Lecture Example 12:14
- Lecture Example 24:12
- Lecture Example 310:06
- Additional Example 4-1
- Additional Example 5-2
31m 13s
- Intro0:00
- Definition and Theorem0:05
- Monotonically Increasing0:25
- Monotonically Decreasing0:40
- Monotonic0:48
- Bounded1:00
- Theorem1:11
- Lecture Example 11:31
- Lecture Example 211:06
- Lecture Example 314:03
- Additional Example 4-1
- Additional Example 5-2
31m 46s
- Intro0:00
- Important Definitions0:05
- Sigma Notation0:13
- Sequence of Partial Sums0:30
- Converging to a Limit1:49
- Diverging to Infinite2:20
- Geometric Series2:40
- Common Ratio2:47
- Sum of a Geometric Series3:09
- Test for Divergence5:11
- Not for Convergence6:06
- Lecture Example 18:32
- Lecture Example 210:25
- Lecture Example 316:26
- Additional Example 4-1
- Additional Example 5-2
23m 26s
- Intro0:00
- Important Theorem and Definition0:05
- Three Conditions0:25
- Converging and Diverging0:51
- P-Series1:11
- Lecture Example 12:19
- Lecture Example 25:08
- Lecture Example 36:38
- Additional Example 4-1
- Additional Example 5-2
22m 44s
- Intro0:00
- Important Tests0:01
- Comparison Test0:22
- Limit Comparison Test1:05
- Lecture Example 11:44
- Lecture Example 23:52
- Lecture Example 36:01
- Lecture Example 410:04
- Additional Example 5-1
- Additional Example 6-2
25m 26s
- Intro0:00
- Main Theorems0:05
- Alternation Series Test (Leibniz)0:11
- How It Works0:26
- Two Conditions0:46
- Never Use for Divergence1:12
- Estimates of Sums1:50
- Lecture Example 13:19
- Lecture Example 24:46
- Lecture Example 36:28
- Additional Example 4-1
- Additional Example 5-2
33m 27s
- Intro0:00
- Theorems and Definitions0:06
- Two Common Questions0:17
- Absolutely Convergent0:45
- Conditionally Convergent1:18
- Divergent1:51
- Missing Case2:02
- Ratio Test3:07
- Root Test4:45
- Lecture Example 15:46
- Lecture Example 29:23
- Lecture Example 313:13
- Additional Example 4-1
- Additional Example 5-2
38m 36s
- Intro0:00
- Main Definitions and Pattern0:07
- What Is The Point0:22
- Radius of Convergence Pattern0:45
- Interval of Convergence2:42
- Lecture Example 13:24
- Lecture Example 210:55
- Lecture Example 314:44
- Additional Example 4-1
- Additional Example 5-2
30m 18s
- Intro0:00
- Taylor and Maclaurin Series0:08
- Taylor Series0:12
- Maclaurin Series0:59
- Taylor Polynomial1:20
- Lecture Example 12:35
- Lecture Example 26:51
- Lecture Example 311:38
- Lecture Example 417:29
- Additional Example 5-1
- Additional Example 6-2
50m 50s
- Intro0:00
- Main Formulas0:06
- Alternating Series Error Bound0:28
- Taylor's Remainder Theorem1:18
- Lecture Example 13:09
- Lecture Example 29:08
- Lecture Example 317:35
- Additional Example 4-1
- Additional Example 5-2
For more information, please see full course syllabus of College Calculus: Level II
College Calculus: Level II Taylor Series and Maclaurin Series
In this video we are going to take a look at Taylor Series and Maclaurin Series. Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point. If the Taylor series is centered at zero, then that series is also called a Maclaurin series. So the Maclaurin series is just a special case of Taylor series. We are also going to talk about Taylor Polynomials. The formula for the Taylor Polynomial looks exactly the same for the Taylor series, except what we do is instead of running it to infinity, we cut the thing off at the degree k term.
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
- - Allow users to view the embedded video in full-size.










































 Answer Engine
Answer Engine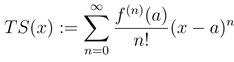 .
.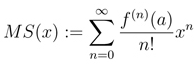 .
.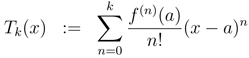
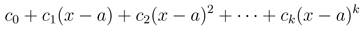






1 answer
Wed Mar 8, 2017 1:26 PM
Post by Chris Ouyang on March 6, 2017
Hello Dr William Murray
Would the trick you used in example 6 still work if it was a Taylor series not centered around 0?
3 answers
Mon Feb 1, 2016 5:56 PM
Post by Luvivia Chang on January 22, 2016
Hello Dr. William Murray,
This is Luvivia again. I haven't had courses on educator.com for a long time and I just want to come back to say Thank You.
I got a 5 in my AP Calculus BC test. Honestly your lectures were all I got when I taught myself calculus and prepared for the exam last year. I found them quite helpful, especially for students like me who are interested in calculus but can't find any concerning courses offered in school. Thank you for your excellent lectures and all your patience in answering me questions. I really appreciate the long answers you've written.
I wish you all the best.
Yours sincerely,
Luvivia
1 answer
Fri Nov 27, 2015 9:08 PM
Post by Chonglin Xu on November 23, 2015
From 20:27 to 20:28, why did the video screen briefly fade out?
1 answer
Wed Oct 14, 2015 4:09 PM
Post by Shehryar Khursheed on October 12, 2015
What is a safe n to stop at to determine the pattern of the series?
3 answers
Sat Apr 25, 2015 7:34 PM
Post by Luvivia Chang on April 18, 2015
Hello Dr William Murray
Before this lecture, I regarded Cn as a constant in the series. But judging from what I learned from this lecture, it seems that Cn changes as n changes. Is that right?
And I find it tricky to use x in the series. Because x has long been used as an unknown or variable in many algebra problems such as functions and equations. But it seems that x here is a coefficient and that only if x has a certain value will the whole series be determined. Am I understanding it correctly?
Thank you.
1 answer
Tue May 28, 2013 7:06 PM
Post by Luis Chanez on May 27, 2013
You are very smart professor Murray. I past my calculus II class
I am looking forward in taking differential equations with you
Thanks fort everything :)
1 answer
Mon Dec 3, 2012 5:29 PM
Post by Louise Barrea on December 3, 2012
Isn't there a mistake a the end of the lecture? When sec x = 1 + .... instead of sec x = 1/ (1+ ....).
1 answer
Mon Dec 3, 2012 5:27 PM
Post by khadar mire on November 14, 2011
Many thanks
2 answers
Tue Nov 20, 2012 6:41 PM
Post by nicholas devos on April 18, 2011
there is a problem at 15:48. Where n=2, the denominator should be 4, not 2.