

Professor Switkes
Review of Functions
Slide Duration:Table of Contents
26m 29s
- Intro0:00
- What is a Function0:10
- Domain and Range0:21
- Vertical Line Test0:31
- Example: Vertical Line Test0:47
- Function Examples1:57
- Example: Squared2:10
- Example: Natural Log2:41
- Example: Exponential3:21
- Example: Not Function3:54
- Odd and Even Functions4:39
- Example: Even Function5:10
- Example: Odd Function5:53
- Odd and Even Examples6:48
- Odd Function6:55
- Even Function8:43
- Increasing and Decreasing Functions10:15
- Example: Increasing10:42
- Example: Decreasing10:55
- Increasing and Decreasing Examples11:41
- Example: Increasing11:48
- Example: Decreasing12:33
- Types of Functions13:32
- Polynomials13:45
- Powers14:06
- Trigonometric14:34
- Rational14:50
- Exponential15:13
- Logarithmic15:29
- Lecture Example 115:55
- Lecture Example 217:51
- Additional Example 3-1
- Additional Example 4-2
12m 29s
- Intro0:00
- Compositions0:09
- Alternative Notation0:32
- Three Functions0:47
- Lecture Example 11:19
- Lecture Example 23:25
- Lecture Example 36:45
- Additional Example 4-1
- Additional Example 5-2
20m 59s
- Intro0:00
- Rates of Change0:11
- Average Rate of Change0:21
- Instantaneous Rate of Change0:33
- Slope of the Secant Line0:46
- Slope of the Tangent Line1:00
- Lecture Example 11:14
- Lecture Example 26:36
- Lecture Example 311:30
- Additional Example 4-1
- Additional Example 5-2
22m 37s
- Intro0:00
- What is a Limit?0:10
- Lecture Example 10:56
- Lecture Example 25:28
- Lecture Example 39:27
- Additional Example 4-1
- Additional Example 5-2
28m 19s
- Intro0:00
- Evaluating Limits0:09
- Lecture Example 11:06
- Lecture Example 25:16
- Lecture Example 38:15
- Lecture Example 412:58
- Additional Example 5-1
- Additional Example 6-2
23m 39s
- Intro0:00
- Formal Definition0:13
- Template0:55
- Epsilon and Delta1:24
- Lecture Example 11:40
- Lecture Example 29:20
- Additional Example 3-1
- Additional Example 4-2
19m 9s
- Intro0:00
- Continuity0:13
- Continuous0:16
- Discontinuous0:37
- Intermediate Value Theorem0:52
- Example1:22
- Lecture Example 12:58
- Lecture Example 29:02
- Additional Example 3-1
- Additional Example 4-2
22m 52s
- Intro0:00
- Limit Definition of the Derivative0:11
- Three Versions0:13
- Lecture Example 11:02
- Lecture Example 24:33
- Lecture Example 36:49
- Lecture Example 410:11
- Additional Example 5-1
- Additional Example 6-2
26m 1s
- Intro0:00
- Power Rule of Differentiation0:14
- Power Rule with Constant0:41
- Sum/Difference1:15
- Lecture Example 11:59
- Lecture Example 26:48
- Lecture Example 311:22
- Additional Example 4-1
- Additional Example 5-2
14m 54s
- Statement of the Product Rule0:08
- Lecture Example 10:41
- Lecture Example 22:27
- Lecture Example 35:03
- Additional Example 4-1
- Additional Example 5-2
19m 17s
- Intro0:00
- Statement of the Quotient Rule0:07
- Carrying out the Differentiation0:23
- Quotient Rule in Words1:00
- Lecture Example 11:19
- Lecture Example 24:23
- Lecture Example 38:00
- Additional Example 4-1
- Additional Example 5-2
17m 43s
- Intro0:00
- Rates of Change0:11
- Lecture Example 10:44
- Lecture Example 25:16
- Lecture Example 37:38
- Additional Example 4-1
- Additional Example 5-2
26m 58s
- Intro0:00
- Six Basic Trigonometric Functions0:11
- Patterns0:47
- Lecture Example 11:18
- Lecture Example 27:38
- Lecture Example 312:15
- Lecture Example 414:25
- Additional Example 5-1
- Additional Example 6-2
23m 47s
- Intro0:00
- Statement of the Chain Rule0:09
- Chain Rule for Three Functions0:27
- Lecture Example 11:00
- Lecture Example 24:34
- Lecture Example 37:23
- Additional Example 4-1
- Additional Example 5-2
27m 5s
- Intro0:00
- Six Basic Inverse Trigonometric Functions0:10
- Lecture Example 11:11
- Lecture Example 28:53
- Lecture Example 312:37
- Additional Example 4-1
- Additional Example 5-2
15m 52s
- Intro0:00
- Point Slope Form0:10
- Lecture Example 10:47
- Lecture Example 23:15
- Lecture Example 36:10
- Additional Example 4-1
- Additional Example 5-2
30m 5s
- Intro0:00
- Purpose0:09
- Implicit Function0:20
- Lecture Example 10:32
- Lecture Example 27:14
- Lecture Example 311:22
- Lecture Example 416:43
- Additional Example 5-1
- Additional Example 6-2
13m 16s
- Intro0:00
- Notation0:08
- First Type0:19
- Second Type0:54
- Lecture Example 11:41
- Lecture Example 23:15
- Lecture Example 34:57
- Additional Example 4-1
- Additional Example 5-2
17m 42s
- Intro0:00
- Essential Equations0:12
- Lecture Example 11:34
- Lecture Example 22:48
- Lecture Example 35:54
- Additional Example 4-1
- Additional Example 5-2
14m 30s
- Intro0:00
- Essential Equations0:15
- Six Basic Hyperbolic Trigc Functions0:32
- Six Basic Inverse Hyperbolic Trig Functions1:21
- Lecture Example 11:48
- Lecture Example 23:45
- Lecture Example 37:09
- Additional Example 4-1
- Additional Example 5-2
29m 5s
- Intro0:00
- What Are Related Rates?0:08
- Lecture Example 10:35
- Lecture Example 25:25
- Lecture Example 311:54
- Additional Example 4-1
- Additional Example 5-2
23m 52s
- Intro0:00
- Essential Equations0:09
- Linear Approximation (Tangent Line)0:18
- Example: Graph1:18
- Differential (df)2:06
- Delta F5:10
- Lecture Example 16:38
- Lecture Example 211:53
- Lecture Example 315:54
- Additional Example 4-1
- Additional Example 5-2
18m 57s
- Intro0:00
- Minimums and Maximums0:09
- Absolute Minima and Maxima (Extrema)0:53
- Critical Points1:25
- Lecture Example 12:58
- Lecture Example 26:57
- Lecture Example 310:02
- Additional Example 4-1
- Additional Example 5-2
20m
- Intro0:00
- Theorems0:09
- Mean Value Theorem0:13
- Graphical Explanation0:36
- Rolle's Theorem2:06
- Graphical Explanation2:28
- Lecture Example 13:36
- Lecture Example 26:33
- Lecture Example 39:32
- Additional Example 4-1
- Additional Example 5-2
27m 11s
- Intro0:00
- Local Minimum and Local Maximum0:14
- Example1:01
- First and Second Derivative Test1:26
- First Derivative Test1:36
- Example2:00
- Second Derivative Test (Concavity)2:58
- Example: Concave Down3:15
- Example: Concave Up3:54
- Inconclusive4:19
- Lecture Example 15:23
- Lecture Example 212:03
- Lecture Example 315:54
- Additional Example 4-1
- Additional Example 5-2
23m 9s
- Intro0:00
- Using L'Hopital's Rule0:09
- Informal Definition0:34
- Lecture Example 11:27
- Lecture Example 24:00
- Lecture Example 35:40
- Lecture Example 49:38
- Additional Example 5-1
- Additional Example 6-2
40m 16s
- Intro0:00
- Collecting Information0:15
- Domain and Range0:17
- Intercepts0:21
- Symmetry Properties (Even/Odd/Periodic)0:33
- Asymptotes (Vertical/Horizontal/Slant)0:45
- Critical Points1:15
- Increasing/Decreasing Intervals1:24
- Inflection Points1:38
- Concave Up/Down1:52
- Maxima/Minima2:03
- Lecture Example 12:58
- Lecture Example 210:52
- Lecture Example 317:55
- Additional Example 4-1
- Additional Example 5-2
25m 37s
- Intro0:00
- Real World Problems0:08
- Sketch0:11
- Interval0:20
- Rewrite in One Variable0:26
- Maximum or Minimum0:34
- Critical Points0:42
- Optimal Result0:52
- Lecture Example 11:05
- Lecture Example 26:12
- Lecture Example 313:31
- Additional Example 4-1
- Additional Example 5-2
25m 13s
- Intro0:00
- Approximating Using Newton's Method0:10
- Good Guesses for Convergence0:32
- Lecture Example 10:49
- Lecture Example 24:21
- Lecture Example 37:59
- Additional Example 4-1
- Additional Example 5-2
36m 50s
- Intro0:00
- Three Approximations0:12
- Right Endpoint, Left Endpoint, Midpoint0:22
- Formulas1:05
- Velocity and Distance1:35
- Lecture Example 12:28
- Lecture Example 212:10
- Lecture Example 319:43
- Additional Example 4-1
- Additional Example 5-2
22m 2s
- Intro0:00
- Important Equations0:22
- Riemann Sum0:28
- Integral1:58
- Integrand2:35
- Limits of Integration (Upper Limit, Lower Limit)2:43
- Other Equations3:05
- Fundamental Theorem of Calculus4:00
- Lecture Example 15:04
- Lecture Example 210:43
- Lecture Example 313:52
- Additional Example 4-1
- Additional Example 5-2
23m 19s
- Intro0:00
- U-Substitution0:13
- Important Equations0:30
- Purpose0:36
- Lecture Example 11:30
- Lecture Example 26:17
- Lecture Example 39:00
- Lecture Example 411:24
- Additional Example 5-1
- Additional Example 6-2
19m 59s
- Intro0:00
- Area Between Two Curves0:12
- Graphic Description0:34
- Lecture Example 11:44
- Lecture Example 25:39
- Lecture Example 38:45
- Additional Example 4-1
- Additional Example 5-2
24m 22s
- Intro0:00
- Important Equations0:16
- Equation 1: Rotation about x-axis (disks)0:27
- Equation 2: Two curves about x-axis (washers)3:38
- Equation 3: Rotation about y-axis5:31
- Lecture Example 16:05
- Lecture Example 28:28
- Lecture Example 311:55
- Additional Example 4-1
- Additional Example 5-2
30m 29s
- Intro0:00
- Important Equations0:50
- Equation 1: Rotation about y-axis1:04
- Equation 2: Rotation about y-axis (2 curves)7:34
- Equation 3: Rotation about x-axis8:15
- Lecture Example 18:57
- Lecture Example 214:26
- Lecture Example 318:15
- Additional Example 4-1
- Additional Example 5-2
16m 31s
- Intro0:00
- Important Equations0:11
- Origin of Formula0:34
- Lecture Example 12:51
- Lecture Example 25:30
- Lecture Example 38:13
- Additional Example 4-1
- Additional Example 5-2
23m 58s
- Intro0:00
- Slope Function of f(x)0:41
- Slope is Zero0:53
- Slope is Positive1:03
- Slope is Negative1:13
- Slope Function of f'(x)1:31
- Slope is Zero1:42
- Slope is Positive1:48
- Slope is Negative1:54
- Lecture Example 12:23
- Lecture Example 28:06
- Lecture Example 312:36
- Additional Example 4-1
- Additional Example 5-2
18m 32s
- Intro0:00
- Things to Remember0:13
- Graphic Description0:42
- Lecture Example 11:44
- Lecture Example 26:59
- Lecture Example 39:46
- Additional Example 4-1
- Additional Example 5-2
17m 4s
- Intro0:00
- Differential Equations0:10
- Focus on Exponential Growth/Decay0:27
- Separating Variables0:47
- Lecture Example 11:35
- Lecture Example 26:41
- Lecture Example 39:36
- Additional Example 4-1
- Additional Example 5-2
For more information, please see full course syllabus of College Calculus: Level I
College Calculus: Level I Review of Functions
In this video, we are going to do a quick review of functions. First, we will see what the function is and what the domain and range of function are. We will see how to determine whether the y is a function of x or not using the Vertical Line Test. Then we will see some examples of functions and their roughly drawn sketches. After that we are going to talk about some other descriptive terms of functions like Odd and Even functions or Increasing and Decreasing functions. At the end, we are going to review types of functions and do some examples.
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
- - Allow users to view the embedded video in full-size.










































 Answer Engine
Answer Engine
 0Graph
0Graph  0Graph
0Graph  0Graph
0Graph  0Graph
0Graph  0Simplify
0Simplify  0Find the asymptote(s) of
0Find the asymptote(s) of  0Graph
0Graph 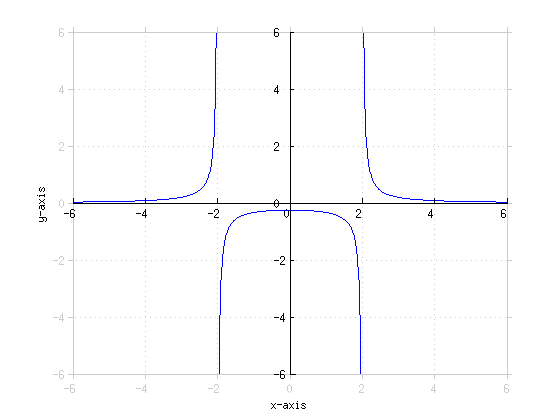 0Graph
0Graph 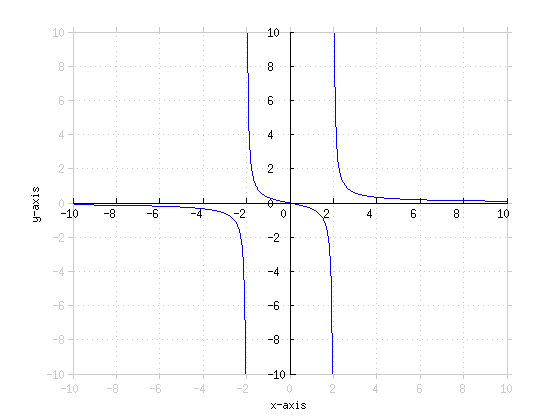 0Graph
0Graph 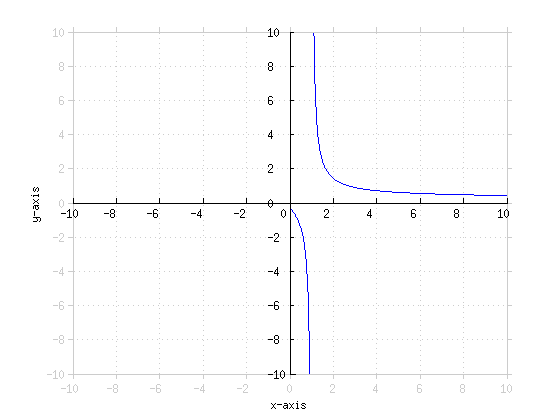






1 answer
Mon Nov 12, 2018 6:57 PM
Post by Karoly Ficsor on August 5, 2018
why is it not possible to view Additional Examples 3 and 4?
0 answers
Post by Mohamed E Sowaileh on July 10, 2017
Hello Dr. Jenny Switkes,
I hope you are very well.
I am a student who is extremely weak in math. In order to be very strong in math, specially for engineering field, could you provide me with sequential order of mathematical topics and textbooks. With what should I begin so that I can master big topics like calculus, statistics, probability ... etc.
Your guidance is precious to me.
Thank you so much.
1 answer
Last reply by: Firebird wang
Wed Nov 2, 2016 9:55 PM
Post by MOHAMMED ALHUMAIDI on June 16, 2016
Please where can I find the downloadable lecture slides?
0 answers
Post by Daniel Gonzalez on June 1, 2016
where can I find the downloadable lecture slides?
1 answer
Last reply by: Bilbo Baggins
Sat Sep 5, 2015 4:19 PM
Post by enya zh on August 19, 2015
You are soooooooooooo much better than Zhu(the person who teaches AP Calculus AB & BC).☺☺☺☺☺☺☺☺
0 answers
Post by Matthew Favazza on January 21, 2015
The watch clinging the screen is very, very distracting...
0 answers
Post by Timothy Davis on August 10, 2014
Hello Professor Switkes
Wouldn't sin(-x) = -sin(-x)? Isn't the definition of an odd function
f(x) = -f(-x)?
1 answer
Last reply by: Hee Su Jang
Mon Jul 14, 2014 6:30 PM
Post by Taylor Wright on August 7, 2013
At 12:30
Why would it not include zero?
if x=0, then the sqrt of zero is zero, which would be included in the function.
1 answer
Last reply by: Taylor Wright
Wed Aug 7, 2013 1:49 AM
Post by Maureen Dempsey on March 27, 2013
hi what is the difference between exponenial and power function....don't they both involve an exponent? She didn't really clarify how they are different. thanks for a great tutoria otherwise.
0 answers
Post by Eun Jee Kang on October 9, 2012
I can't continue the lesson after odd and even examples. Please check it out. i don't know what problem is.
0 answers
Post by Jacob Mack on August 8, 2012
y = x^2 + 1 would be a function but y^2 = x + 1 is not. To see this algebraically instead of geometrically we can plug a number in for x for the first equation, say, 2, so 2 squared is four + 1 is 5. We have exactly one value of x domain we get one output of y in the equation. Thus, 2^2 + 1 = 5 is a function. Plugging in 3 for the second equation we see it is not a function: y^2 = 3 + so y can be = 2 or -2, therefore there are two outputs from the range y of the equation.
0 answers
Post by Jacob Mack on August 8, 2012
In general, any equation can yield a corresponding graph and any graph can be represented by a corresponding equation. Like y = x^2 yields the familiar parabola.
For y = log(x) we can break it apart to be y = f(x) = 1n(x) + x and then move on to solve geometrically.
0 answers
Post by Jason Mannion on October 4, 2011
Video works fine for me so far. Hope to get a better handle on Calculus now!
0 answers
Post by Marsha Taylor on January 23, 2011
These videos are a great for learning math or for review.
0 answers
Post by NICK FOSTER on January 20, 2011
no iam sorry about that comment everything is ok the videos play and are amazing!!keep up the good job