

Professor Switkes
Algebraic Evaluation of Limits
Slide Duration:Table of Contents
26m 29s
- Intro0:00
- What is a Function0:10
- Domain and Range0:21
- Vertical Line Test0:31
- Example: Vertical Line Test0:47
- Function Examples1:57
- Example: Squared2:10
- Example: Natural Log2:41
- Example: Exponential3:21
- Example: Not Function3:54
- Odd and Even Functions4:39
- Example: Even Function5:10
- Example: Odd Function5:53
- Odd and Even Examples6:48
- Odd Function6:55
- Even Function8:43
- Increasing and Decreasing Functions10:15
- Example: Increasing10:42
- Example: Decreasing10:55
- Increasing and Decreasing Examples11:41
- Example: Increasing11:48
- Example: Decreasing12:33
- Types of Functions13:32
- Polynomials13:45
- Powers14:06
- Trigonometric14:34
- Rational14:50
- Exponential15:13
- Logarithmic15:29
- Lecture Example 115:55
- Lecture Example 217:51
- Additional Example 3-1
- Additional Example 4-2
12m 29s
- Intro0:00
- Compositions0:09
- Alternative Notation0:32
- Three Functions0:47
- Lecture Example 11:19
- Lecture Example 23:25
- Lecture Example 36:45
- Additional Example 4-1
- Additional Example 5-2
20m 59s
- Intro0:00
- Rates of Change0:11
- Average Rate of Change0:21
- Instantaneous Rate of Change0:33
- Slope of the Secant Line0:46
- Slope of the Tangent Line1:00
- Lecture Example 11:14
- Lecture Example 26:36
- Lecture Example 311:30
- Additional Example 4-1
- Additional Example 5-2
22m 37s
- Intro0:00
- What is a Limit?0:10
- Lecture Example 10:56
- Lecture Example 25:28
- Lecture Example 39:27
- Additional Example 4-1
- Additional Example 5-2
28m 19s
- Intro0:00
- Evaluating Limits0:09
- Lecture Example 11:06
- Lecture Example 25:16
- Lecture Example 38:15
- Lecture Example 412:58
- Additional Example 5-1
- Additional Example 6-2
23m 39s
- Intro0:00
- Formal Definition0:13
- Template0:55
- Epsilon and Delta1:24
- Lecture Example 11:40
- Lecture Example 29:20
- Additional Example 3-1
- Additional Example 4-2
19m 9s
- Intro0:00
- Continuity0:13
- Continuous0:16
- Discontinuous0:37
- Intermediate Value Theorem0:52
- Example1:22
- Lecture Example 12:58
- Lecture Example 29:02
- Additional Example 3-1
- Additional Example 4-2
22m 52s
- Intro0:00
- Limit Definition of the Derivative0:11
- Three Versions0:13
- Lecture Example 11:02
- Lecture Example 24:33
- Lecture Example 36:49
- Lecture Example 410:11
- Additional Example 5-1
- Additional Example 6-2
26m 1s
- Intro0:00
- Power Rule of Differentiation0:14
- Power Rule with Constant0:41
- Sum/Difference1:15
- Lecture Example 11:59
- Lecture Example 26:48
- Lecture Example 311:22
- Additional Example 4-1
- Additional Example 5-2
14m 54s
- Statement of the Product Rule0:08
- Lecture Example 10:41
- Lecture Example 22:27
- Lecture Example 35:03
- Additional Example 4-1
- Additional Example 5-2
19m 17s
- Intro0:00
- Statement of the Quotient Rule0:07
- Carrying out the Differentiation0:23
- Quotient Rule in Words1:00
- Lecture Example 11:19
- Lecture Example 24:23
- Lecture Example 38:00
- Additional Example 4-1
- Additional Example 5-2
17m 43s
- Intro0:00
- Rates of Change0:11
- Lecture Example 10:44
- Lecture Example 25:16
- Lecture Example 37:38
- Additional Example 4-1
- Additional Example 5-2
26m 58s
- Intro0:00
- Six Basic Trigonometric Functions0:11
- Patterns0:47
- Lecture Example 11:18
- Lecture Example 27:38
- Lecture Example 312:15
- Lecture Example 414:25
- Additional Example 5-1
- Additional Example 6-2
23m 47s
- Intro0:00
- Statement of the Chain Rule0:09
- Chain Rule for Three Functions0:27
- Lecture Example 11:00
- Lecture Example 24:34
- Lecture Example 37:23
- Additional Example 4-1
- Additional Example 5-2
27m 5s
- Intro0:00
- Six Basic Inverse Trigonometric Functions0:10
- Lecture Example 11:11
- Lecture Example 28:53
- Lecture Example 312:37
- Additional Example 4-1
- Additional Example 5-2
15m 52s
- Intro0:00
- Point Slope Form0:10
- Lecture Example 10:47
- Lecture Example 23:15
- Lecture Example 36:10
- Additional Example 4-1
- Additional Example 5-2
30m 5s
- Intro0:00
- Purpose0:09
- Implicit Function0:20
- Lecture Example 10:32
- Lecture Example 27:14
- Lecture Example 311:22
- Lecture Example 416:43
- Additional Example 5-1
- Additional Example 6-2
13m 16s
- Intro0:00
- Notation0:08
- First Type0:19
- Second Type0:54
- Lecture Example 11:41
- Lecture Example 23:15
- Lecture Example 34:57
- Additional Example 4-1
- Additional Example 5-2
17m 42s
- Intro0:00
- Essential Equations0:12
- Lecture Example 11:34
- Lecture Example 22:48
- Lecture Example 35:54
- Additional Example 4-1
- Additional Example 5-2
14m 30s
- Intro0:00
- Essential Equations0:15
- Six Basic Hyperbolic Trigc Functions0:32
- Six Basic Inverse Hyperbolic Trig Functions1:21
- Lecture Example 11:48
- Lecture Example 23:45
- Lecture Example 37:09
- Additional Example 4-1
- Additional Example 5-2
29m 5s
- Intro0:00
- What Are Related Rates?0:08
- Lecture Example 10:35
- Lecture Example 25:25
- Lecture Example 311:54
- Additional Example 4-1
- Additional Example 5-2
23m 52s
- Intro0:00
- Essential Equations0:09
- Linear Approximation (Tangent Line)0:18
- Example: Graph1:18
- Differential (df)2:06
- Delta F5:10
- Lecture Example 16:38
- Lecture Example 211:53
- Lecture Example 315:54
- Additional Example 4-1
- Additional Example 5-2
18m 57s
- Intro0:00
- Minimums and Maximums0:09
- Absolute Minima and Maxima (Extrema)0:53
- Critical Points1:25
- Lecture Example 12:58
- Lecture Example 26:57
- Lecture Example 310:02
- Additional Example 4-1
- Additional Example 5-2
20m
- Intro0:00
- Theorems0:09
- Mean Value Theorem0:13
- Graphical Explanation0:36
- Rolle's Theorem2:06
- Graphical Explanation2:28
- Lecture Example 13:36
- Lecture Example 26:33
- Lecture Example 39:32
- Additional Example 4-1
- Additional Example 5-2
27m 11s
- Intro0:00
- Local Minimum and Local Maximum0:14
- Example1:01
- First and Second Derivative Test1:26
- First Derivative Test1:36
- Example2:00
- Second Derivative Test (Concavity)2:58
- Example: Concave Down3:15
- Example: Concave Up3:54
- Inconclusive4:19
- Lecture Example 15:23
- Lecture Example 212:03
- Lecture Example 315:54
- Additional Example 4-1
- Additional Example 5-2
23m 9s
- Intro0:00
- Using L'Hopital's Rule0:09
- Informal Definition0:34
- Lecture Example 11:27
- Lecture Example 24:00
- Lecture Example 35:40
- Lecture Example 49:38
- Additional Example 5-1
- Additional Example 6-2
40m 16s
- Intro0:00
- Collecting Information0:15
- Domain and Range0:17
- Intercepts0:21
- Symmetry Properties (Even/Odd/Periodic)0:33
- Asymptotes (Vertical/Horizontal/Slant)0:45
- Critical Points1:15
- Increasing/Decreasing Intervals1:24
- Inflection Points1:38
- Concave Up/Down1:52
- Maxima/Minima2:03
- Lecture Example 12:58
- Lecture Example 210:52
- Lecture Example 317:55
- Additional Example 4-1
- Additional Example 5-2
25m 37s
- Intro0:00
- Real World Problems0:08
- Sketch0:11
- Interval0:20
- Rewrite in One Variable0:26
- Maximum or Minimum0:34
- Critical Points0:42
- Optimal Result0:52
- Lecture Example 11:05
- Lecture Example 26:12
- Lecture Example 313:31
- Additional Example 4-1
- Additional Example 5-2
25m 13s
- Intro0:00
- Approximating Using Newton's Method0:10
- Good Guesses for Convergence0:32
- Lecture Example 10:49
- Lecture Example 24:21
- Lecture Example 37:59
- Additional Example 4-1
- Additional Example 5-2
36m 50s
- Intro0:00
- Three Approximations0:12
- Right Endpoint, Left Endpoint, Midpoint0:22
- Formulas1:05
- Velocity and Distance1:35
- Lecture Example 12:28
- Lecture Example 212:10
- Lecture Example 319:43
- Additional Example 4-1
- Additional Example 5-2
22m 2s
- Intro0:00
- Important Equations0:22
- Riemann Sum0:28
- Integral1:58
- Integrand2:35
- Limits of Integration (Upper Limit, Lower Limit)2:43
- Other Equations3:05
- Fundamental Theorem of Calculus4:00
- Lecture Example 15:04
- Lecture Example 210:43
- Lecture Example 313:52
- Additional Example 4-1
- Additional Example 5-2
23m 19s
- Intro0:00
- U-Substitution0:13
- Important Equations0:30
- Purpose0:36
- Lecture Example 11:30
- Lecture Example 26:17
- Lecture Example 39:00
- Lecture Example 411:24
- Additional Example 5-1
- Additional Example 6-2
19m 59s
- Intro0:00
- Area Between Two Curves0:12
- Graphic Description0:34
- Lecture Example 11:44
- Lecture Example 25:39
- Lecture Example 38:45
- Additional Example 4-1
- Additional Example 5-2
24m 22s
- Intro0:00
- Important Equations0:16
- Equation 1: Rotation about x-axis (disks)0:27
- Equation 2: Two curves about x-axis (washers)3:38
- Equation 3: Rotation about y-axis5:31
- Lecture Example 16:05
- Lecture Example 28:28
- Lecture Example 311:55
- Additional Example 4-1
- Additional Example 5-2
30m 29s
- Intro0:00
- Important Equations0:50
- Equation 1: Rotation about y-axis1:04
- Equation 2: Rotation about y-axis (2 curves)7:34
- Equation 3: Rotation about x-axis8:15
- Lecture Example 18:57
- Lecture Example 214:26
- Lecture Example 318:15
- Additional Example 4-1
- Additional Example 5-2
16m 31s
- Intro0:00
- Important Equations0:11
- Origin of Formula0:34
- Lecture Example 12:51
- Lecture Example 25:30
- Lecture Example 38:13
- Additional Example 4-1
- Additional Example 5-2
23m 58s
- Intro0:00
- Slope Function of f(x)0:41
- Slope is Zero0:53
- Slope is Positive1:03
- Slope is Negative1:13
- Slope Function of f'(x)1:31
- Slope is Zero1:42
- Slope is Positive1:48
- Slope is Negative1:54
- Lecture Example 12:23
- Lecture Example 28:06
- Lecture Example 312:36
- Additional Example 4-1
- Additional Example 5-2
18m 32s
- Intro0:00
- Things to Remember0:13
- Graphic Description0:42
- Lecture Example 11:44
- Lecture Example 26:59
- Lecture Example 39:46
- Additional Example 4-1
- Additional Example 5-2
17m 4s
- Intro0:00
- Differential Equations0:10
- Focus on Exponential Growth/Decay0:27
- Separating Variables0:47
- Lecture Example 11:35
- Lecture Example 26:41
- Lecture Example 39:36
- Additional Example 4-1
- Additional Example 5-2
For more information, please see full course syllabus of College Calculus: Level I
College Calculus: Level I Algebraic Evaluation of Limits
In this lecture we are going to talk about algebraic evaluation of limits. In previous lesson, we were talking about limit investigations and now we will do just a quick review of it. Sometimes, the limit is in a type 0/0 . In these cases, an algebraic rearrangement will help us to evaluate a limit. Our first example will be to compute the limit: lim (x→9)((√x-3)/(x-9)) . This is a 0/0 limit, so called indeterminate type. To solve this, we need to write this limit in some other form using algebraic tricks. Further steps are shown in video. Additional examples are also included.
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
- - Allow users to view the embedded video in full-size.










































 Answer Engine
Answer Engine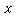 approaches
approaches 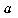 (not what happens at
(not what happens at 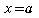 ).
). 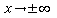 , we are looking at what happens as x increases or decreases without bound.
, we are looking at what happens as x increases or decreases without bound. 





0 answers
Post by Francois Barrett on September 8, 2014
Explained everything thoroughly... If only my calc Prof could do the same
0 answers
Post by Mirza Baig on November 26, 2013
For example 3 can we use l'hopital's rule to figure out the limits ?
0 answers
Post by ALI SAAD on December 2, 2012
She knows the matterial well, But she doesnt know how to explain in,She rather further complicate this.Educator.com must start listining to people's opinion to be able to attract more students!
0 answers
Post by kelly Akum on July 18, 2012
I agree. she does explain things very well.
0 answers
Post by Wayne Phan on March 7, 2012
This material in this video was very well explained. Thank you, Professor! keep up the good work.
0 answers
Post by Nick Kozik on February 20, 2012
LOL at anyone saying this is hard, or that Switkes is a bad teacher. She explains 10 times better than my Calculus teacher, and explains in more detail than he does; and I have had over sixty people tell me my teacher is great.
She gives pleanty of examples, and pleanty of detail...Actually, WAY more detail than needed. Look to the last lesson (Limit Investigations) where she shows compute derivatives, something you may not know. This = More than enough information.
1 answer
Last reply by: Scott Katzelnick
Sat Mar 3, 2012 12:57 AM
Post by arturo torres on January 1, 2012
i feel that for example number one we ignored the fact that sqrt of 9 can also be -3 with would still make this undefined. dose anyone know why we would ignore that?
0 answers
Post by Hamza albobaz on October 29, 2011
thank u verey much keep it up