Kinematic equations are used to describe and analyze motion of particles with constant acceleration. (constant acceleration is an essential assumption. If the body has variable acceleration then we will have to figure out different equations)

Kinematic equations can give us information about five key variables involved with an object in motion. These are

• displacement, ??x
• initial velocity, v_o
• final velocity, v
• acceleration, a
• time, t

All of these variables can be derived from position of the object and time .

In this article we will only deal with motion in a straight line and the kinematic equations describing such motion.

Kinematic Equations

The three kinematic equations are as follows:

Deriving Kinematic Equations:

1.

We know that acceleration is constant.

Acceleration is as we know is the difference in velocity over time.

Difference in velocity:

So if write the equation for acceleration:

 
 

 
 
which is our first kinematic equation

2.
 
 
In this equation, we find the change in position.

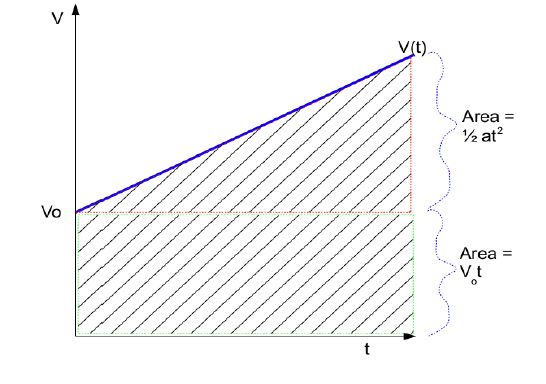
We know that in a velocity time graph, the area under the curve gives us the change in position.

So if we draw a velocity time graph, with initial velocity v_o at time t=0, it will be similar to the graph drawn below. Acceleration is constant, so the slope of the curve is constant.

Now to find the area, we divide the region into a triangle and a rectangle.

The area of the rectangle is :

Area of triangle:

 
 

 
 
base = t
 
 
So,
 
 

 
 

total area gives:

 
 
Which is the second equation

Now for this equation we must remember the following relations,

now if we replace a in the second kinematic equation by the first relation, we get

 
 

 
 

 
 

 
 
Now we take this equation and multiply it with the first equation.

We get,

 
 
and with appropriate algebraic manipulation as follows,

Thus we get our third kinematic equation,

1. Another equation we use along with the other three equations, is the following

Problem Solving

Now armed with these equations, we are going to see how we can analyze and solve problems involving objects in motion with constant acceleration.

We need to systematically analyze the problem to arrive at solutions.

For that we will go through the following steps:

• Figure out whether the problem involves motion in vertical or horizontal axis.

For example a ball thrown upwards would consist of motion in only vertical axis.

Similarly cars moving on plane road would consist of motion on a horizontal axis.

For our current discussion we will only consider motion in a straight line.

• Choose a direction as positive

After we select an axis, we need to assign one direction as positive and the other direction as negative. We can select any direction as positive, so long as we are careful to not change it in the middle of solving a particular problem.

To make things easier, in this article we will consider the direction in which the object initially starts moving as positive. You can try solving the same problems assigning the opposite direction as positive and see if there is any difference!

• Create a motion analysis table

Now we make a table and note the variables for initial velocity (V_o), final velocity (V), displacement (?x or ?y), acceleration (a) and time (t).

• Figure out all the known variables

We now figure out which all variables have values given in the question and which variables are unknown.

• Solve the equation for the unknown variable.

In this last step we need to select the kinematic equation such that only one variable is unknown.

After we solve the equation, we can figure out the unknown variable.

A variety of solved examples, nicely explained can be found in the lecture, AP Physics 1 & 2 Kinematic Equations

We will solve a few more here.

Q1) Suppose a car is travelling at 20m/s. But it accelerates by 2m/s² for 50meters before settling down at some constant velocity. For how long did it accelerate and what is the final velocity after this acceleration?

ANS) So the velocity is horizontal so we will consider it in x-axis.

We can make the car go either to the right or to the left. Let us for convenience decide it is going to the right and make right the positive direction.

Initial velocity , v₀ = 20m/s

acceleration, a =2m/s²

?x = 50m

Now we can use the equation

substituting the values will give us the equation as –

 
 

 
 
which is a quadratic equation.

Solving this equation using algebraic methods gives us a positive solution and a negative solution. We know that time difference is obviously positive, so we take the positive solution, t = 2.25s

So the car accelerated for 2.25 seconds

Then we can use the equation

Which means the final stable velocity after acceleration was 24.5m/s

Q2) A little kid dropped a glass plate from the top of a building and heard it hit the ground and break after 2s. If the height of the building is 19.6m, what was the acceleration of the plate while it fell down?

ANS)We now have the displacement of the object and time interval. Since the plate was dropped, we assume the initial velocity to be zero.

So,

 
 

 
 

 
 
So we use the equation,

Substituting the values:

So we see the acceleration is 9.8m/s²

Free fall

What we just saw in the above example is known as a free fall.

When the only force acting on an object is the earth’s gravitational force, we say that the object is in a free fall.

When the only force acting on the object is the earth’s gravitational force; the acceleration experienced due to this force is uniform for all objects independent of its mass. (This is explained in the chapter ‘Gravitation‘)

But if we throw a paper ball and heavy stone, we can see that the stone is falling faster. If they have same initial velocity and and same acceleration, then they should fall together!

Well this happens because apart from the earth’s gravitational pull, the two objects experience air resistance. Air resistance slows down the paper ball more than it slows down the stone. (Sky divers take advance of this very air resistance and slow down their fall with help of parachutes).

But if we remove air from a place completely (create vacuum), all objects will definitely experience the same acceleration! And fall at the same rate! In vacuum, a feather and a bowling ball will both drop together if initial velocity is same!

For now we will ignore air resistance. So the only force acting will be the force of gravity and hence all objects under free fall will have the same acceleration.

At the surface of the earth, the value of this acceleration is 9.8m/s² and is commonly referred to as ‘g‘ – free fall acceleration. The direction of acceleration is always downwards.

We will from time approximate the value of ‘g‘ to 10m/s²

Objects falling from rest

Lets see what happens if an object is dropped down.

The initial velocity is then zero.

Since the objects starts the motion in downward direction, we can take this direction to be positive.

Acceleration (g) is also in downward direction, so it is positive.

So a=+9.8m/s²

Objects thrown upwards

When objects are thrown upwards they start with a velocity V_o, with which they are thrown.

Since initial velocity is upwards, we can consider the upward direction as positive.

Now since the acceleration is downwards, it is in negative direction.

So a=-9.8m/s² and since it is in opposite direction to the initial velocity, it slows the object down.

Now we know that objects keep going up till a certain height, then starts falling back again when we throw them upwards.

At the highest point, the upward velocity slows down to zero and then the object then begins it descent with velocity in the downward direction. So at the highest point, for an instance, the object has zero velocity.

Lets see two examples of objects in free fall:

Q1) Bob is at the top of a tower which is 45m tall. Alice is standing some distance away from the base of the tower. If Bob drops an apple by mistake and it is falling towards the base of the tower, how much time does Alice have to move to the base of the tower if she wants to prevent the apple from hitting the ground? [Take g=10m/s²]

ANS) So we have an object falling from rest.

So we take downwards as the positive direction. So a= +10m/s²

 
 

 
 

 
 
We use the equation,

and substitute the values

So, we take the positive value , t=3s. So Alice has to reach the base of the tower within 3 seconds of Bob dropping the apple.

Q2) If Alice throws the apple upwards with an initial velocity o f 25m/s, will it reach Bob? If not, what maximum height will it reach? [Take g=10m/s²]

ANS) Now the initial velocity is upwards. So we take upwards as the positive velocity.

But g is downwards. So a = -10m/s²

We also know that at the highest position, the velocity of the object is zero. So if we consider the motion of the apple from its initial velocity till when it reaches maximum height, we can take final velocity as zero.

We use the equation,

Substituting the values

So it won’t reach Bob.

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our AP Physics 1 & 2 course. We cover topics such as Kinematic Equation.[/box]