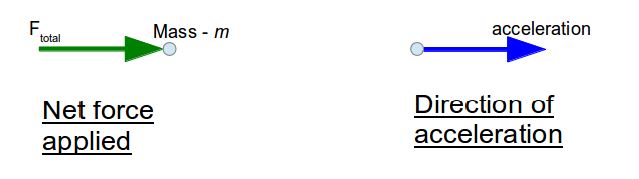In this article we are going to state and understand Newton’s second law of motion. But before we do, we will go through some important concepts which will help us understand Newton’s second law efficiently.

Free Body Diagram

Let us first understand what is a Free-Body-Diagram (FBD).

Free-Body-Diagrams are diagrams which show all the forces that are acting on a particular body.

The diagram conventionally denotes the object as a dot (or as a box or any other symbol) and then arrows are used to show all the forces acting on that body.

Thus diagram ONLY SHOWS the object and the forces acting on it and nothing else.

Only one object or body is analysed in a FBD at a time.

The drawing of a free-body diagram is an important step in the solving of mechanics problems since it helps us visualize all the forces acting on a single object.

Let us now see a few examples of FBDs.

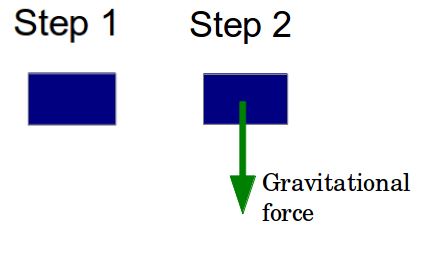
• Let’s say a box is free falling from a height under the influence of gravity.

1. So we draw the body (the box) first.
2. Then we indicate the force due to gravity by an arrow.

And thus we have our first Free-Body-Diagram!!

It is as simple as that!

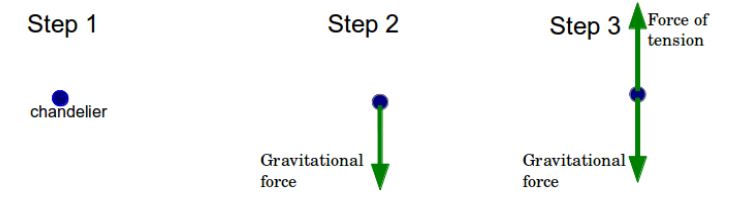
• Let us take another example of a chandelier hanging from the ceiling. Can we draw a FBD of that?

1. Let us represent the chandelier by a dot in our FBD.
2. Next we are going to draw an arrow downwards showing the gravitational force acting on the chandelier.
3. Now the chandelier is attached to to the ceiling through some rope or chain. Let us just for the sake of this example assume its a tight rope. So this rope pulls the chandelier upwards and prevents it from falling down.
4. This force (genrally when a rope or string pulls something) is known as the force of tension. So we draw an arrow showing the force due to tension upwards.

We can see that the chandelier does not fall down, which means that the gravitational force must be balanced by the force due to tension in the rope!

And so we have drawn our second FBD!

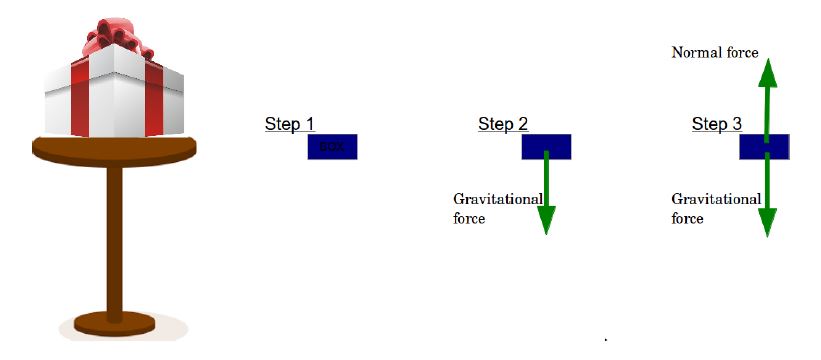
• Let’s see another example of a box on a table.

1. Like the previous examples we can denote the box as dot or a rectangular box.
2. Then we draw an arrow denoting the gravitational force acting on the box downward.
3. Now since the box is stationary, we know that there must be a force acting upwards which balances the gravitational force on the box. This force is provided by the surface of the table in upward direction and is called normal force. (‘normal’ denotes perpendicular to surface)
4. So we draw an arrow denoting the normal force.

NOTE: The normal force always acts on an object in a direction which is perpendicular to the surface on which the object is placed.

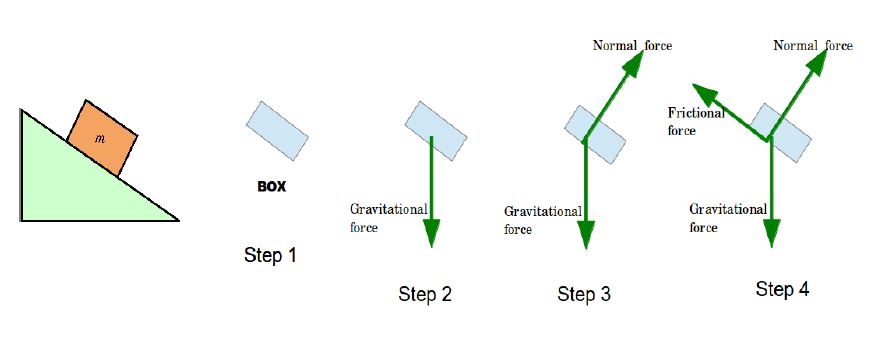
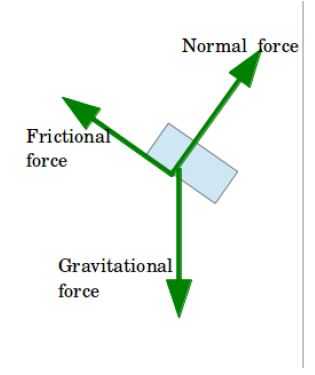
Now let’s see an example where the forces might not be aligned in the same line.

• An object sliding down a ramp at an angle.

1. Again as in previous example we denot the object as an rectangular box.
2. We show the gravitational force with a downward arrow.
3. Now the surface of the ramp is at an angle, so the normal force on the box can be shown by an arrow pointing perpendicularly outwards from the surface.
4. Since the box is sliding down, there will be a frictional force opposite to the direction of its movement, along the surface.

The diagram in step-4 shows us the final FBD

But we see a slight problem here!

The forces are not aligned and are in different direction!

To figure out what is the net force on the object and whether the object is in equililibrium, we draw pseudo FBDs.

Pseudo FBD

In psudo free-body-diagrams we break up the forces into their components along X and Y axis. Then we can deal with the components on X and Y axis separately and find out the net force on the object.

So let us see the previous example of object on a ramp again.

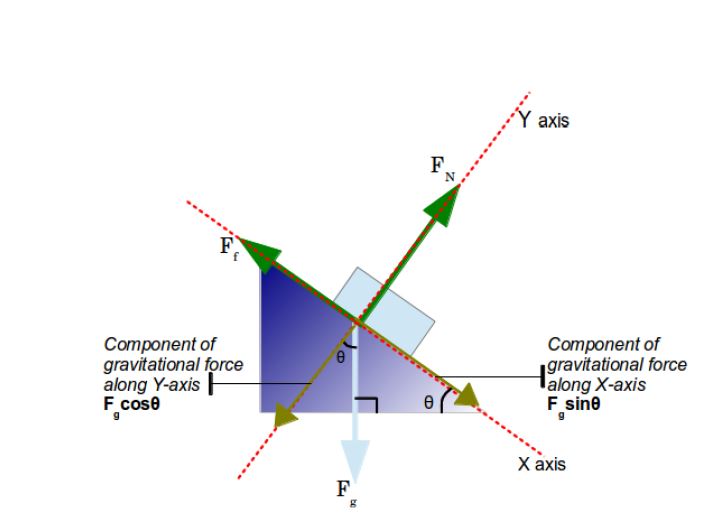
We can select an X-Y axis like we normally do.

In which case the gravitational force will be on the Y-axis only and we will have to break up the Normal and Frictional force into their X and Y components.

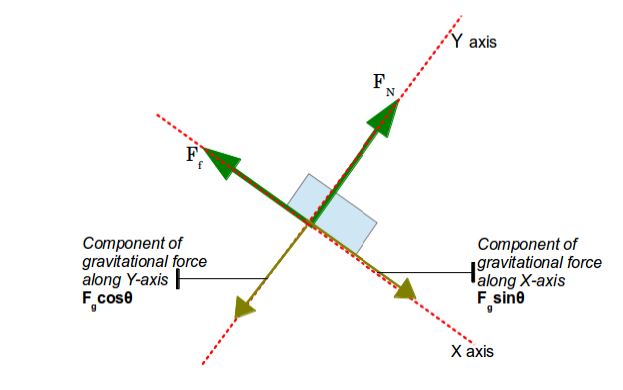
But instead if we select a slightly different set of axes where the X-axis is along the surface of the ramp and the Y-axis is perpendicular to it, then we only have to break up the Gravitational force into its components!

We will call the Normal Force as F_N

The Gravitational Force as F_g

and the Frictional Force as F_f

So we see the ramp makes an angle ? with the horizontal ground. So using this angle we break up the gravitational force into two components
 
 

 
 
Then the pseudo FBD will only contain these component forces along the axes and not Fg in downwards direction.

Pseudo FBD

So in X axis we have :

and in Y axis we have :

And the Net Force is vector sum of Fx and Fy.

Newton’s 2^nd Law Of Motion

The acceleration of an object is in the direction of and directly proportional to the net force applied, and inversely proportional to the object’s mass.

This is perhaps one of the most important laws in classical mechanics.

Suppose we have an object with mass m on which net force applied is F_total in some direction, as in the diagram. Then the acceleration will be in the same direction. It will also be directly proportional to the force F_total and inversely proportional to its mass.

So

Now

and

So we have the equation

Or in its most famous form:

Since its a vector equation, the direction of net force applied gives us the direction of acceleration.

Comparison of Newton’s First and Second Laws of Motions

Applications of Newton’s second Law

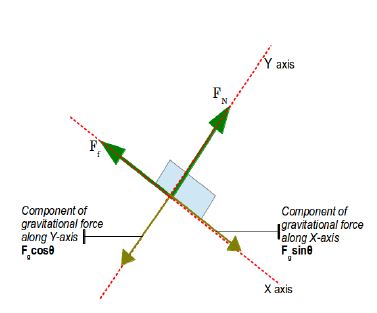1) Let us see the example of the block on the inclined ramp for which we drew the pseudo FBD.

If the block has mass of 5kg and is sliding along the ramp at 1m/s² along the surface, then what is the net force being applied to the block?

ANS) Now we can see from the diagram that X-axis is along the surface and Y axis is perpendicular to the surface of the ramp.

Since there is no acceleration along the Y-axis, net force along Y-axis must be zero.

Now acceleration along the X-axis is 1m/s²

Net force is F_gsin? – F_f

Lets call this Fnet

We will use the equation

with m = 5kg and a = 1m/s²

We have

So net force is 5N

which also means

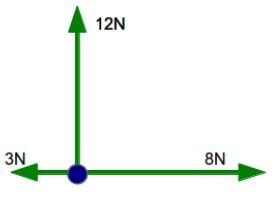
2) Now lets say there is a box on a frictionless surface. There is force of 12N towards north, 8N to the east and 3N to the west. If the box weighs 6.5kg, what would be its accelartion?

ANS) First step is to draw a FBD.

We can see from diagram that force along X-axis is:

8N-3N = 5N

and along Y-axis is : 12N

taking their vector sum gives us

Now we have net force.

We know mass is 6.5kg

So, putting these values in equation

Mass and Weight

Mass – Mass is simply the amount of matter in an object. A stone will have the same mass on earth or anywhere in space.

Weight – Weight is the amount of gravitational force on a body due to its mass. So on the earth’s surface where g=9.8m/s², weight of an object with mass ‘m’ (mg) will be more than its weight on moon where g is considerably lesser.

In space where there might be practically no gravitational field, the weight of the body will be 0, since g=0m/s².

Equilibrium

Equilibrium is generally a state when the object is stable.

Translational equilibrium is when the net force on an object is zero.

We already came across this concept when dealing with Newton’s First Law of Motion.

Equilibrant – equilibrant is the single force applied on an object to make the net force on that object zero.

So if we have a force mg pulling an object of mass m downwards, we can apply an equilibrant force of magnitude mg in upwards direction to reduce the net force to zero!

Let’s see another example.

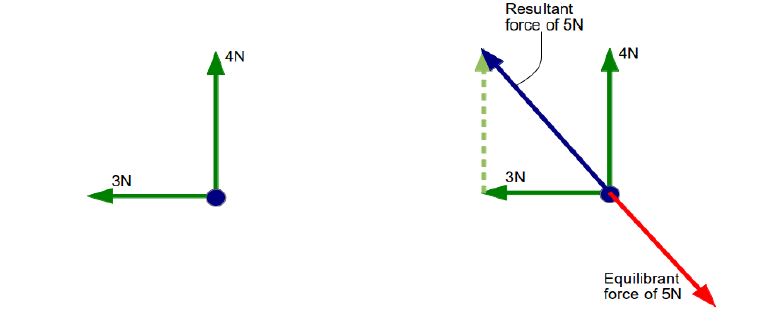
If a force of 4N is being applied to the north and force of 3N is being applied to the west on an object. What will be the Equilibrant force on the object so that net force is zero?

Using vector addition we calculate the resultant force of 4N to north and 3N to west

 
 
So resultant force is 5N in the north-west direction.

So equilibrant force will be 5N in the opposite direction

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our AP Physics 1 & 2 course. We cover topics such as Newton’s 2nd Law of Motion.[/box]