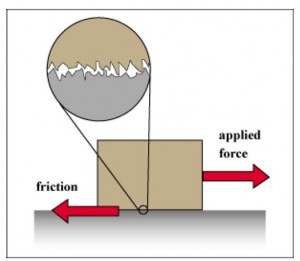
We encounter frictional forces in our daily lives. The force of resistance that you feel when you drag or push a box across the floor is due to the frictional force that occur at the surfaces of the box and the floor which are in contact. Frictional forces help us walk, run, ride a bike and perform a variety of other tasks in our daily lives. Frictional forces exist between surfaces of solid as well as fluid material.

Origin

Friction arises from the very small irregularities that exist on the surfaces in contact.

Frictional force depends on the load of the object. In particular, it is directly proportional to the force exerted due to the weight of the object perpendicularly on the surface (known as Normal Force).

Normal Force

Since frictional force is directly proportional to the normal force, it is important that one should understand normal force.

What exactly is ‘Normal Force’ ?

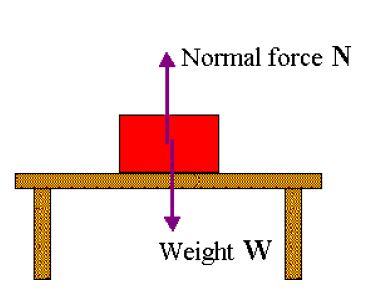
If a stationary object is placed on a surface then it will exert a force equivalent to its weight on the surface. According to Newton’s Third Law, then the surface should exert an equal force on the object too.

This force, exerted by the surface on the object is known as Normal Force. Since the net force vertically is then zero, the object does not move up or down.

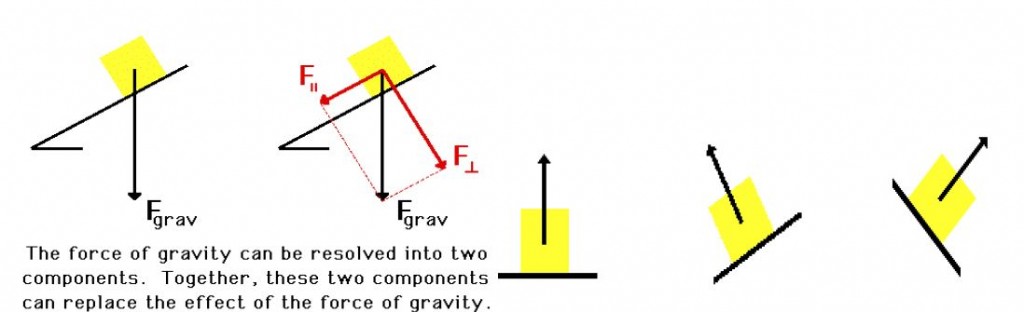
But sometimes, objects are not placed vertically on the surface. The weight of the object then has a component perpendicular to the surface and a component parallel to the surface. The normal force is always equal in magnitude to the perpendicular component of the force exerted by the object on the surface and opposite in direction to it.

Coefficient of Friction

So now we know that frictional forces:

• Oppose any kind of motion and is opposite in direction to the force that might be responsible for the motion of the object, and

• Are directly proportional to the magnitude of the normal force between the surface and object:

[latex  latex size=”2″]F_\text{friction} \propto N[/latex]

So we have an idea about the direction and magnitude of the frictional force.

[latex  latex size=”2″]F_\text{friction} = \mu N[/latex]

We use ? as the constant of proportionality and thus frictional force is given as:

? is a property of the surfaces which are in contact and is known as ‘Coefficient of friction‘.

Types of Frictional Force

• Static Frictional Force
• Kinetic Frictional Force

Surfaces have different coefficients for static and kinetic friction. The coefficient for static friction for a surface is generally higher than the coefficient for kinetic friction.

Static Friction

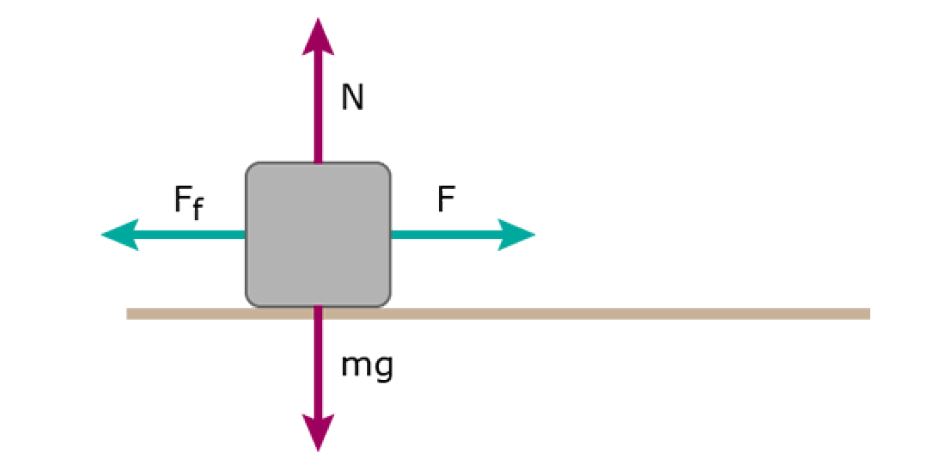
Static friction is the friction force between two surfaces that are not moving relative to each other. For example when you try to move a heavy box and it doesn’t move, it’s the static friction which is at work preventing motion.

The frictional force by static friction neutralises the applied force and hence the net force is zero, which prevents the heavy box from moving from its stationary state.

Static frictional force does not have a constant magnitude but varies according to the applied force so that the net force is always zero. But it does have a maximum value

[latex  latex size=”2″]F_\text{static friction} \le \mu_s N = F_\text{max}[/latex]

Where ?s is the coefficient of static friction and F_max is the maximum static frictional force for the particular pair of surfaces.

Kinetic Friction

What happens when we apply a force greater than F_max ? The net force is not zero anymore and the object starts moving.

The frictional force between surfaces which are moving relative to each other is called Kinetic friction .

[latex  latex size=”2″]F_\text{kinetic friction} =\mu_k N [/latex]

Here ?k is the coefficient of Kinetic friction.

The value of ?k typically is independent of the relative speed of motion of the two surfaces.

Calculation of Frictional Force

To calulate frictional force we need to first find the Normal Force between the surfaces in contact where frictional force occurs. Normal force as we discussed is equal in magnitude to the force applied by the object on the surface, but in opposite direction. Then Frictional force is simply given by:

[latex  latex size=”2″]F_\text{friction} =\mu N [/latex]

(Remember this is not a vector equation, so direction of Normal force and frictional force are different )

The choice of ? depends on the pair of surfaces and whether the surfaces are moving or stationary, relative to each other.

Examples

We can solve two simple examples to see how frictional force is calculated.

i. Movement in horizontal surface

Question: If a box has mass m, coefficient of static friction is ?s, coefficient of kinetic friction for surface is ?k. Then how much force do we need to apply to make the box move from its stationary position? What is the frictional force after it starts moving?

Answer: Lets calculate the normal force first. Here the force exerted by the block on the surface is only due to its weight. If the mass of the block is ‘m’ then weight = mg [where ‘g’ is the gravitational acceleration] Therefore Normal force = mg. Then the maximum static frictional force is given by

[latex  latex size=”2″]F_\text{max} =\mu_s N [/latex]

[latex  latex size=”2″]F_\text{max} =\mu_s mg [/latex]

So we need to apply apply a force greater than this to make the box move. After it starts moving the frictional force is given by kinetic friction.

So [latex  latex size=”2″]F_\text{friction} =\mu_k N = \mu_k mg [/latex] after its starts moving.

ii. Movement in inclined plane

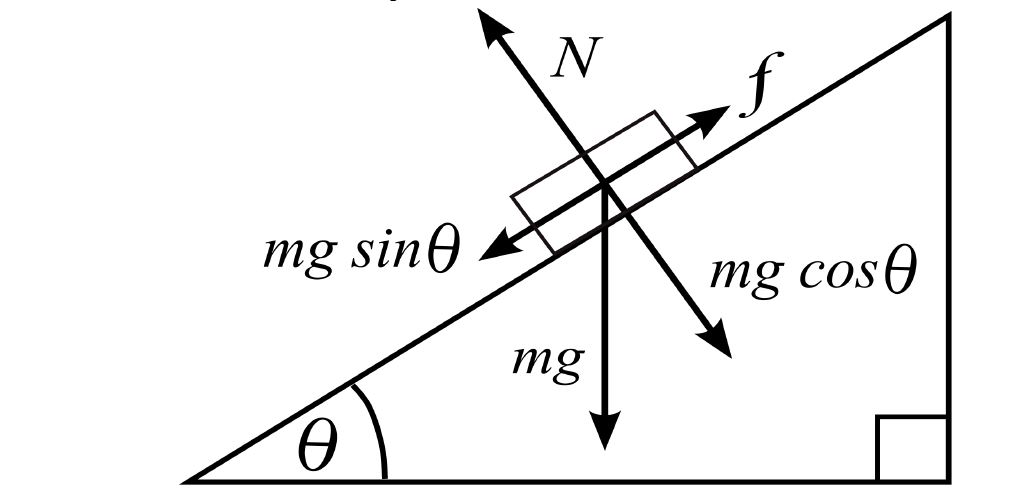
Question: If a box of mass ‘m’ is slipping at the surface of an inclined plane at an angle ?, What is the force of friction, given the coefficient of kinetic friction is ?.

Answer: Lets calculate the normal force. The weight of the box = mg but the force ‘mg’ has a component parallel to the sliding surface and a component perpendicular to the sliding surface. We are only interested in the perpendicular component as that gives the magnitude of the normal force.

Perpendicular component = mg cos?

if N = normal force then N = mg cos?

Now Kinetic Friction = [latex  latex size=”2″]\mu_k N =\mu_k mg \cos \theta[/latex]

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our AP Physics 1 & 2 course. We cover topics such as Friction and Ideal Gases.[/box]