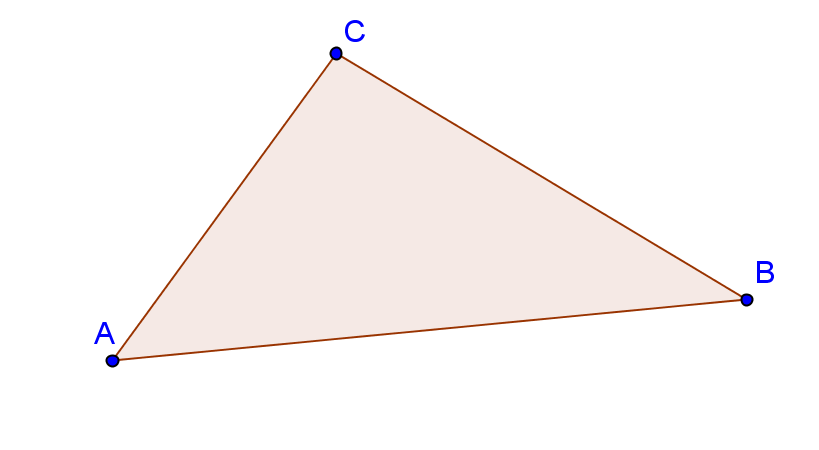
The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

AB + BC > AC

BC + AC > AB

AC + AB > BC

Why is this important?

If any of these three inequalities is not true, you do not have a triangle.

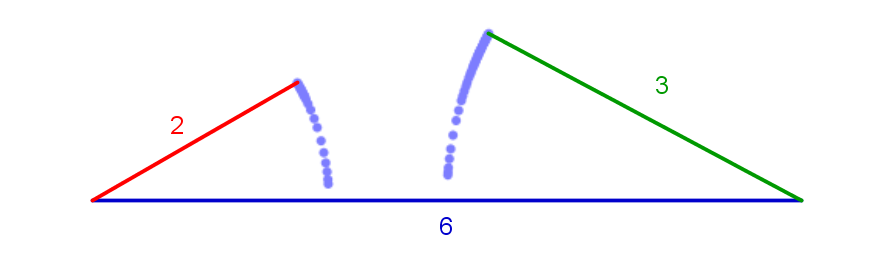
For example, let 2,3 and 6 be the given lengths. Let’s check if they can form a triangle by applying the triangle inequality:

2 + 6 > 3 ?

3 + 6 > 2 ?

2 + 3 > 6 ?

The last inequality is not true and therefore the three given lengths cannot form a triangle. We can graph the given lengths to better understand what this means.

Conclusion: Not any three lengths can be lengths of sides of a triangle. They need to satisfy the triangle inequality.

Note: that you don’t always have to check all three inequalities; it is enough to check if the sum of the two shorter sides is greater then the largest side of a triangle.

Example I

Could a triangle have side lengths of 1, 5 and 9?

Let’s use the triangle inequality theorem and examine all 3 combinations of the sides:

1 + 9 > 5 ?

 1 + 5 > 9 ?

We see that 1+5 is not greater than 9, so these lengths do not satisfy the theorem and they couldn’t form a triangle. There’s no need to check the third inequality because we already have one that doesn’t satisfy the theorem and that is enough to get the conclusion.

Example II

Could a triangle have side lengths of 5, 9 and 10?

We’ll use the shortcut – we can check if the sum of the two shorter sides is greater than the largest side. If so, a triangle could have side lengths of 5, 9 and 10.

 5 +9 > 10 ?

This is true, so yes, a triangle could have these side lengths.

Example III

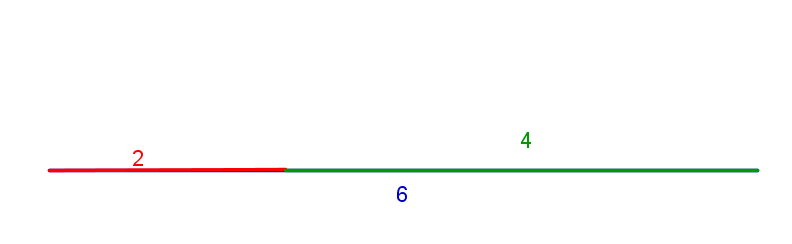
If the sum of two sides is equal to the third side, they still don’t form a triangle. Instead, they form a straight line.

For example, the side lengths of 2, 4 and 6:

2 + 4 > 6 ?

This is incorrect, so the three lengths do not form a triangle.

Did this help?

[box type=”success” align=”” class=”” width=””]Check out more examples in Geometry & 100 other subjects at Educator.com, the best place to get in-depth and instant homework help online.[/box]