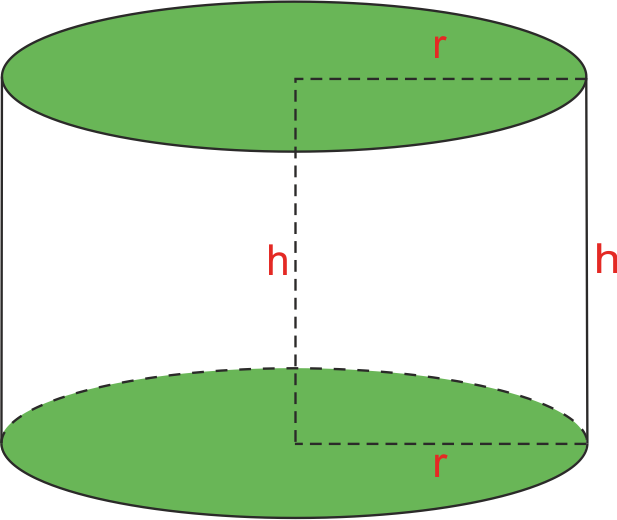
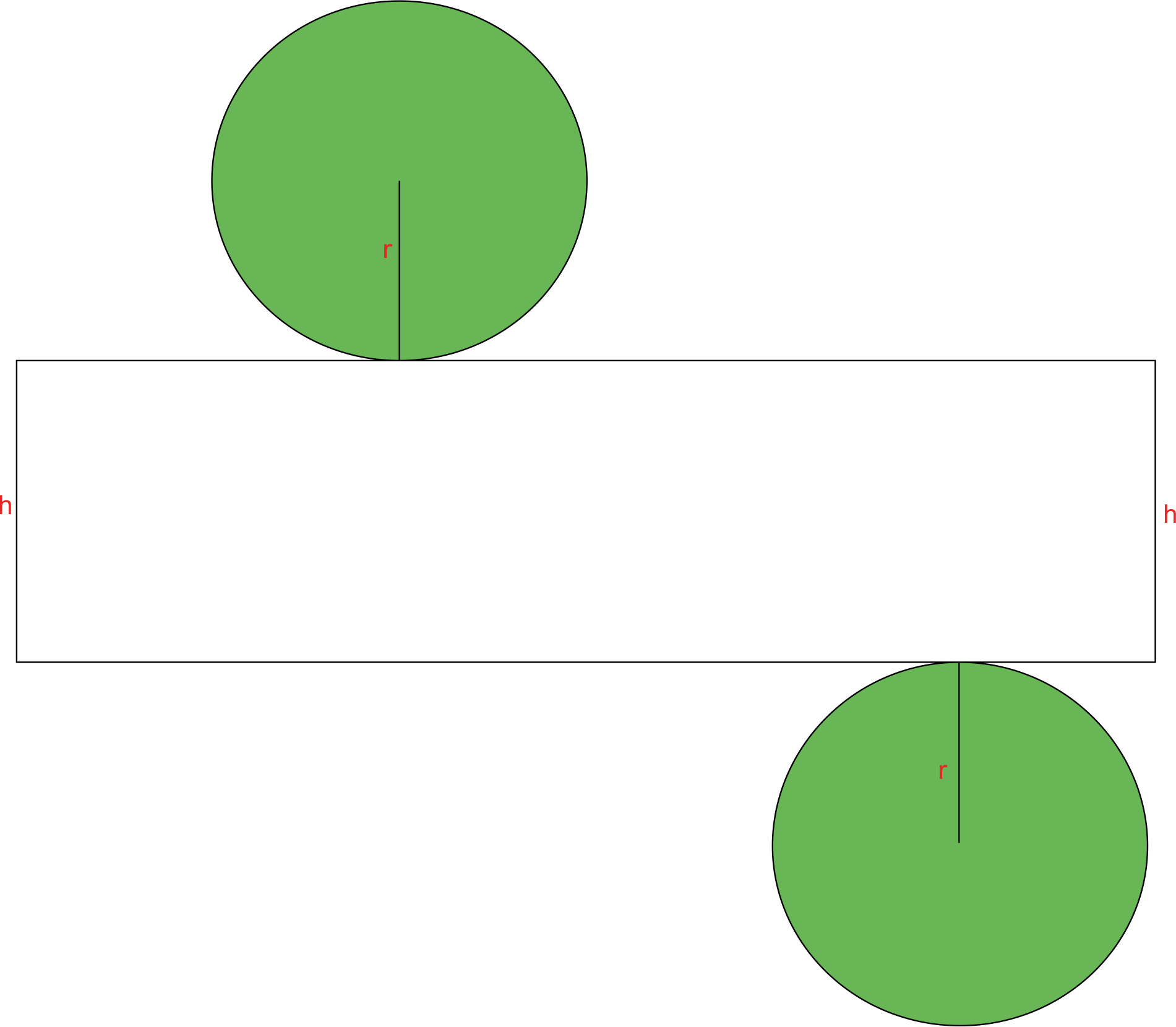
To find the total surface area of a cylinder, we need to find the areas of its three surfaces: the top circle, the bottom circle, and the area in the middle.

The top and the bottom areas are easy to find. Since they are circles, we just use the formula for the area of a circle to find the area of the top and the bottom of a cylinder.

Area of the top = r² ?

Area of the bottom = r² ?

You can see from the picture that r is actually the radius of the base circle.

Now we get to the tricky part, the area in the middle. It’s tricky because it doesn’t have the shape that fits a known area like a triangle or a parallelogram.

To help you visualize this, imagine the cylinder to be a typical can, with a paper label all around its curved wall. If you detached the paper label, it would be in a shape of a rectangle. Its one side would be the height of the cylinder, and since its other side was wrapped around the circle base, its length would be equal to the perimeter of that circle. So, the dimensions of the rectangle (i.e. the area in the middle) would be height of the cylinder and the perimeter of the base.

The picture above shows the net of the cylinder, i.e. how would it look like if we opened it completely.

Now that we know the dimensions of the rectangle in the middle, we can find its area.

The area of a rectangle is length×width.

length = perimeter of the base = 2r?

width = height of a cylinder = h

Area of the middle = 2r? * h

This area is also known as the lateral area.

Finally, if we combine all the three surfaces together, we can get the formula for the total surface area of a cylinder, which is the sum of the three surfaces:

Surface area of a cylinder = r²? + r²? + 2r? * h

And if we simplify it, we get:

Area = 2r²? + 2r? * h

We can write this formula in another way. Notice that both these two summands have 2r? in common, so we can factor it out:

Area = 2r? ( r + h )

These are the two ways to write the formula for the surface area of a cylinder.

Remember: When solving problems that involve the surface area, don’t forget to use the square units.

Example I

A cylinder has a radius of 12 cm and a height of 23 cm. Find it’s surface area (use 3.14 for ?).

We are given r=12 and h=23. Let’s plug it into the formula:

A =2r? ( r + h )

A = 2 * 12 * 3.14 ( 12 + 23 )

A = 75.36 * 35

A = 2637.6 cm²

Example II

As a project in tech class, the students are making aluminum flower pots shaped like cylinders. There is a bottom on each pot, but no top. If the pots are 9″ in height and have a diameter of 12″, how many square inches of aluminum are needed for each pot? (Use 3.14 for ?)

To find the surface area of a cylinder with no top, we will include only one area of a circle (instead of two that we normally include), and a lateral area. Our height is 9, and radius is half a diameter, so radius is 6.

A = r²? + 2r? * h

A = 6² * 3.14 + 2 * 6 * 3.14 * 9

A = 452.16 in²

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our Geometry course. We cover everything from Measuring Segments to Surface Area.[/box]