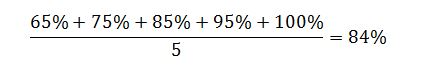You are probably familiar with the arithmetic mean, also known as the average, which is the sum of n numbers divided by n. The geometric mean is another type of mean where we multiply the numbers together and then take the nth root of the product.

So the geometric mean is formally defined as the nth root of the product of n numbers:

For example, the geometric mean of two numbers is a square root of a product of these two numbers, and the geometric mean of five numbers is the fifth root of a product of these five numbers.

So the geometric mean is formally defined as the nth root of the product of n numbers:

Example I

What is the geometric mean of 16 and 4?

The first step is to multiply the numbers: 16 * 4 = 64

Since there are two numbers, the next step is to take the square root of the product: ?64 = 8.

So the geometric mean of 16 and 4 is 8.

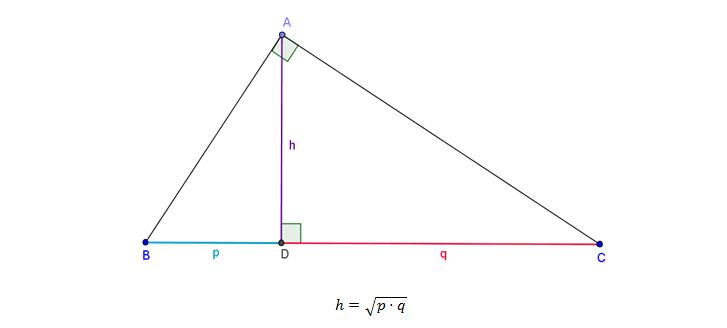
Where does it come from?

The term “geometric mean” comes from geometry. In a right triangle, the height drawn from the vertex of the right angle to the hypotenuse is the geometric mean between the two segments of the hypotenuse:

The formula above can be quickly derived using the Pythagorean theorem, and we will show how in the next few lines.

The difference between arithmetic mean and geometric mean

In order for you to know which one to use, you need to understand the difference between them.

If you were to find the average of your class test scores, you would simply add the scores together and then divide them with the number of terms, to get the average.

For example, if five students took the test and their scores are 65%, 75%, 85%, 95% and 100%, the (arithmetic) average score is:

This solution makes sense because each test score is an independent event. If one student does poorly on the test, that does not affect the other students and their chances of doing poor or well.

However, there are some situations, especially in finance, where using the arithmetic does not make sense, which we’ll see in the next example.

Example II

Let’s say that the returns of your investments for five years are +60%, -50%, +60%, -50% and +60%. The arithmetic average of these returns is 16%, but the geometric average of these same numbers is quite different.

If we write these percentages as numbers, we get 0.6, -0.5, 0.6, -0.5 and 0.6.

1. First add 1 to each number of the sequence (to avoid problems with negative numbers)
2. Find the geometric mean using the formula:
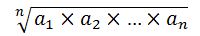
3. Subtract one from the result

Following these steps, we get that the geometric mean of these numbers is 5%, and that is the correct one and the actual return. When it comes to investment returns, the numbers are not independent of each other and thus we have to use the geometric mean.

[box type=”success” align=”” class=”” width=””]Want to learn more? Check out our video lesson on  Geometric Mean for more example problems.[/box]