Polygons are two-dimensional shapes, made of straight lines that connect up and form a closed figure. If a polygon has all sides equal, and all angles equal, it is called a regular polygon. Here we are going to learn how to find the area of a regular polygon.

We are not just going to write down the formula but instead, we are going to see where the formula comes from so that you can learn the idea. This way, even if you forget the formula, and you are in the middle of your exam, you can always easily derive it on a piece of paper.

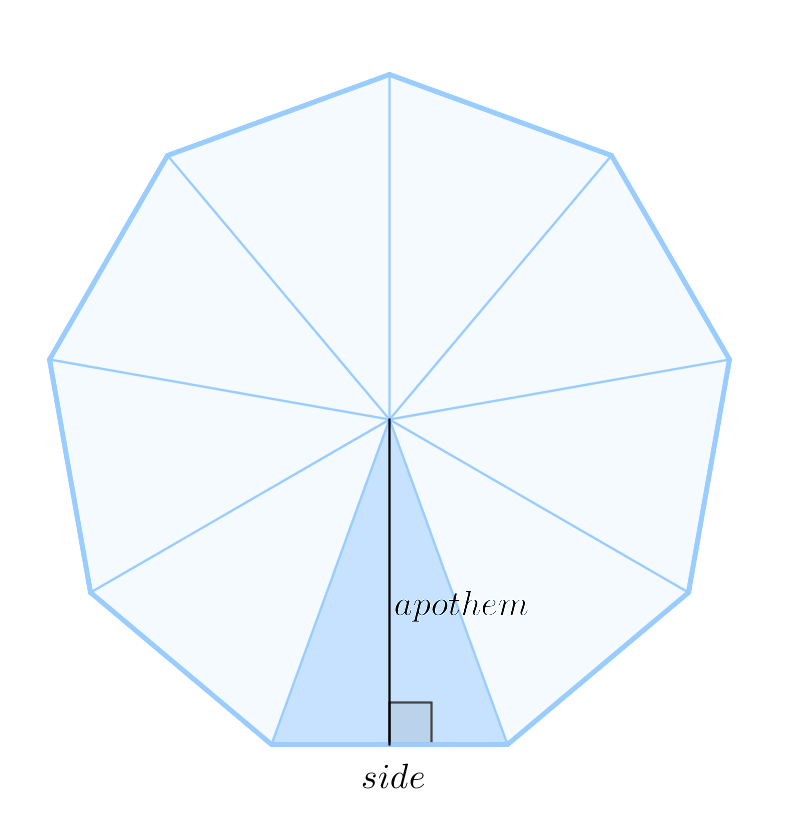
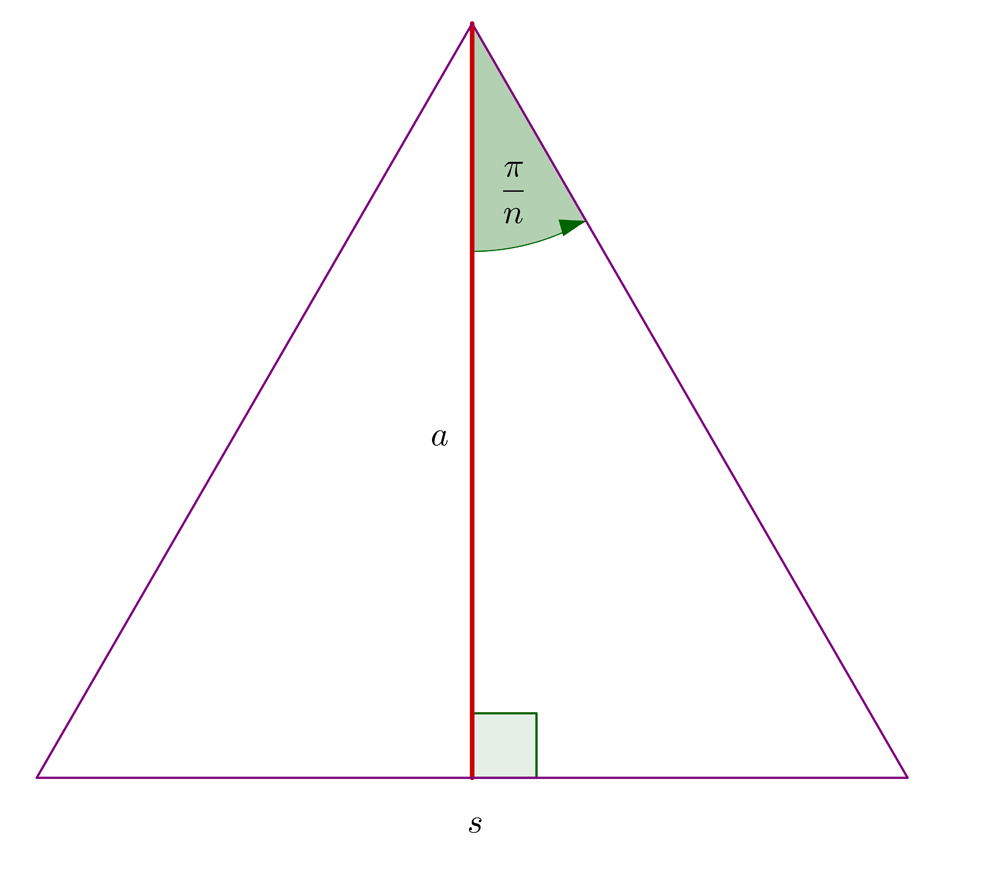
The main idea is to break the polygon down into a set of n isosceles triangles, where n is the number of sides. So for example, we would break down a hexagon into six isosceles triangles. If we can calculate the area of one of the triangles, we can multiply it by n to find the total area of the polygon.

There are three different situations that can occur. You could be given:

1. the side length
2. the radius
3. the apothem

You could, of course, be given all of the data above, and we will consider that case as well.

1. The General Formula

If we break the polygon down into these triangles, we can notice that:

• the base of the triangle is the side of the polygon
• the height of the triangle is the apothem of the polygon

Now, recall the formula for the area of a triangle:

[latex  latex size=”1″]\text{Area of One Triangle} = \frac{1}{2} \ \text{base} \times \text{height} =\frac{1}{2} \ \text{side} \times \text{apothem} [/latex]

To get the area of the entire polygon, we add up the areas of the small triangles (there are n of them):

[latex  latex size=”2″]\text{Area of One Triangle} = n \times \frac{1}{2} \ \text{side} \times \text{apothem} [/latex]

The perimeter of a polygon is the sum of its sides, which is n × side  in this case, so we get:

[latex  latex size=”2″]\text{Area of One Triangle} = \frac{1}{2} \cdot \text{apothem} \cdot \text{perimeter} [/latex]

2. If you are given the side length

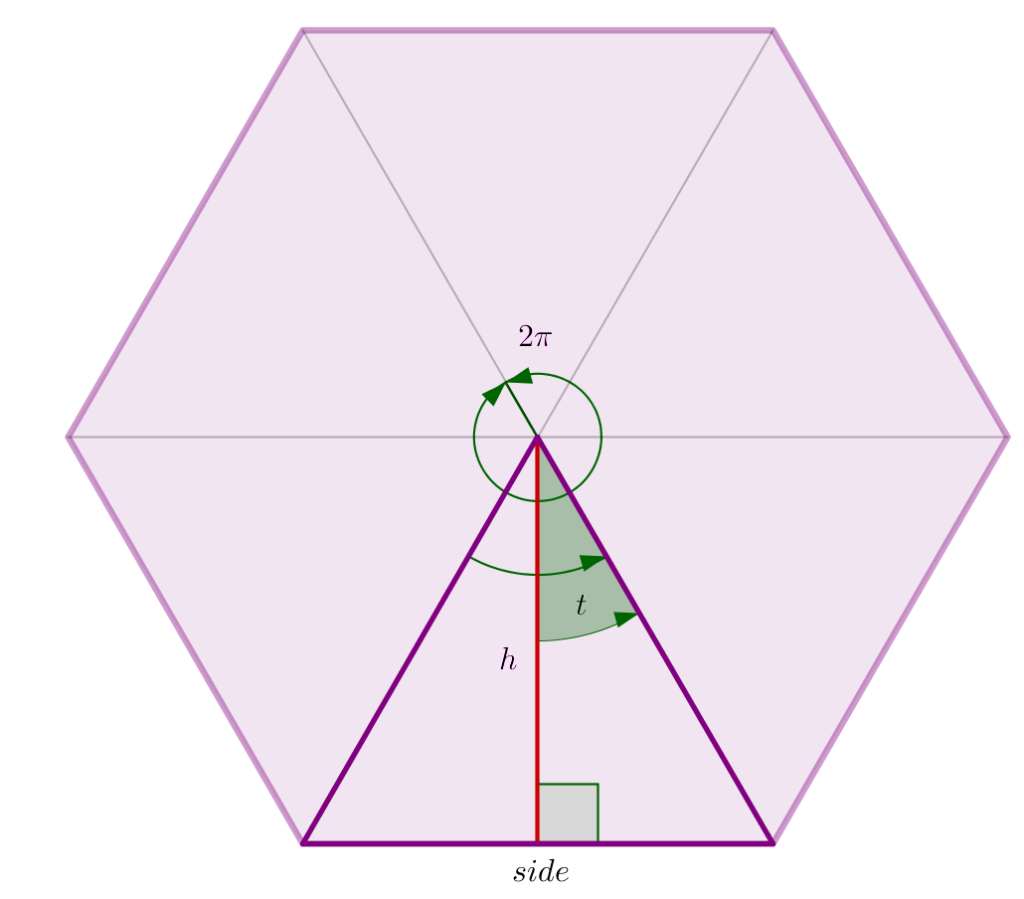
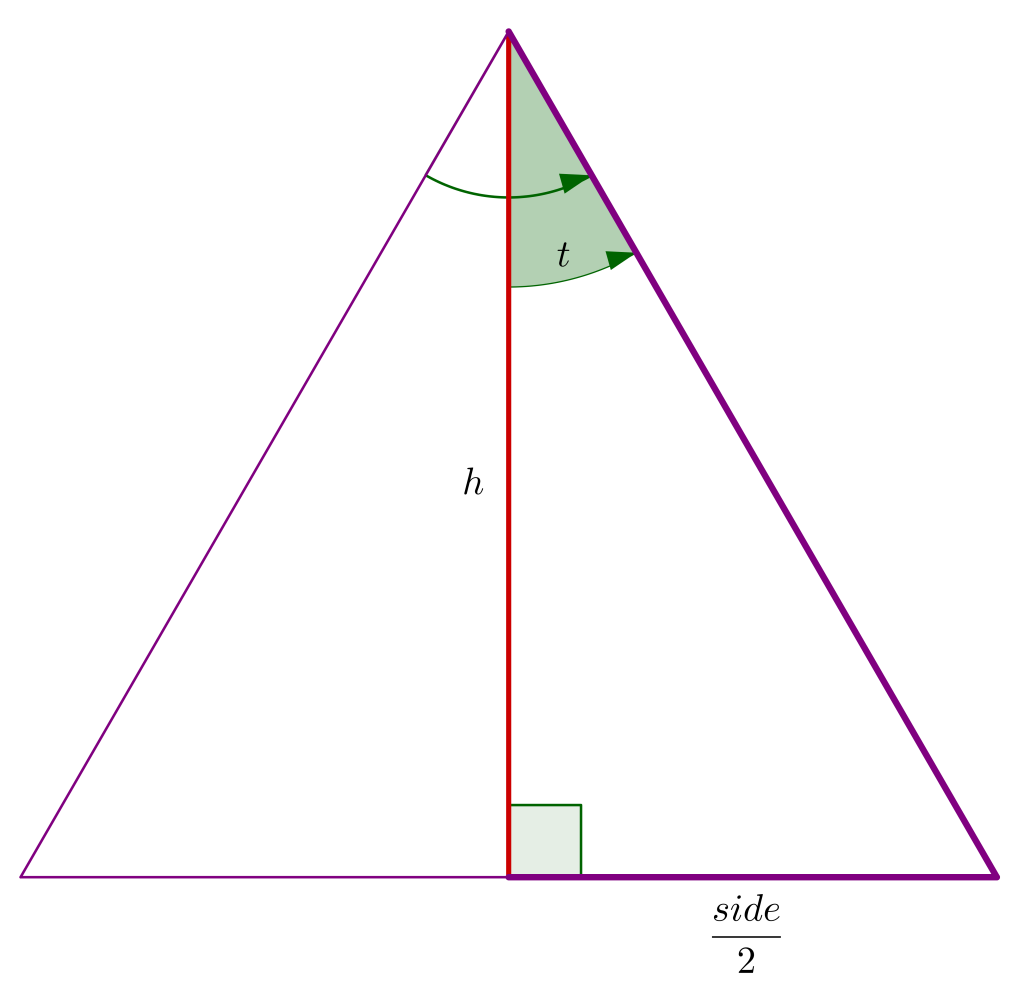
Let’s look at one of the triangles and draw a line from the apex to the midpoint of the base. This line is the height (h) of the triangle, and it forms a right angle with the base. (Remember that we are given the base.)

The angle at the apex is dependent on the number of sides n. To calculate it, we simply divide 2? by the number of sides: (2?)/n  . The angle t is half that, which is

[latex  latex size=”2″]t = \frac{\pi}{n}[/latex]

For example, a hexagon has six sides (n=6), so the angle t in a hexagon is  ?/6.

Our goal is to find the length of the height, so now we need the trigonometry of the right triangle (remember SOHCAHTOA):

[latex  latex size=”2″]\tan \ t = \frac{\text{opposite}}{\text{adjacent}}[/latex]

Since the height bisects the side of our polygon, the opposite side of the angle t is one-half of the given side:

[latex  latex size=”2″]\tan \ t = \frac{\frac{\text{side}}{2}}{h}[/latex]

Solve the formula for h:

[latex  latex size=”2″]h = \frac{\frac{\text{side}}{2}}{\tan \ t }[/latex]

Now let’s find the area of our triangle:

[latex  latex size=”2″]\text{Area of a Triangle} = \frac{1}{2} \cdot \text{base} \cdot \text{height}[/latex]

[latex  latex size=”2″]\text{Area of a Triangle} = \frac{1}{2} \cdot \text{side} \cdot \frac{\frac{\text{side}}{2}}{\tan \ t}[/latex]

We can use s for side:

[latex  latex size=”2″]\text{Area of a Triangle} = \frac{1}{2} \cdot \frac{\frac{s \cdot s}{2}}{\tan \ t}[/latex]

[latex  latex size=”2″]\text{Area of one Triangle} = \frac{s^{2}}{4 \ \tan \ t}[/latex]

Finally, since the polygon has n such triangles, we’ll multiply by n:

[latex  latex size=”2″]\text{Area of a Regular Polygon} = \frac{n \cdot s^{2}}{4 \ \tan \ t}[/latex]

3. If you are given the radius

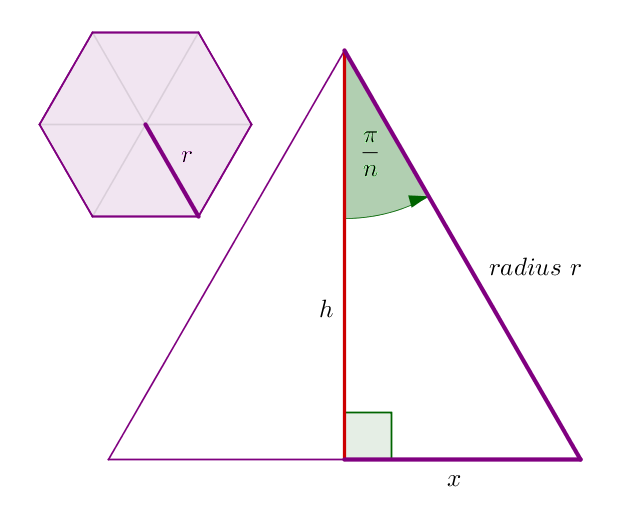
The radius of a regular polygon is the distance from the center to any vertex.

Again, our goal is to find the area of this triangle. We are now given the radius, which is the hypotenuse of the right triangle formed by h and x. Using SOHCAHTOA, we know that:

[latex  latex size=”2″]h = r \cdot \cos\frac{\pi}{n}[/latex]

[latex  latex size=”2″]x = r \cdot \sin\frac{\pi}{n}[/latex]

The area of any triangle is one-half of base times the height. We already have one-half of base, that is the x, so the area of this triangle is:

[latex  latex size=”2″]\text{Area of a Triangle} = x \cdot h[/latex]

[latex  latex size=”2″]\text{Area of a Triangle} = r^{2}\cdot \sin\frac{\pi}{n}\cos\frac{\pi}{n}[/latex]

Using a double angle trigonometric identity, this formula becomes:

[latex  latex size=”2″]\text{Area of a Triangle} = r^{2}\cdot\frac{1}{2}\sin\frac{2\pi}{n}[/latex]

Finally, since the polygon has n such triangles, we’ll multiply by n:

[latex  latex size=”2″]\text{Area of a Regular Polygon} = \frac{1}{2}r^{2} \cdot n \cdot \sin\frac{2\pi}{n}[/latex]

4. If you are given the apothem

The apothem of a regular polygon is a line from the center to the midpoint of a side. (That is actually the height of a triangle.) We’ll use a for apothem and s for the side.

Using SOHCAHTOA we can find the length of the side:

[latex  latex size=”2″]\tan\frac{\pi}{n} = \frac{\frac{s}{2}}{a}[/latex]

Solving this for s we get:

[latex  latex size=”2″]s =2a \cdot \tan\frac{\pi}{n}[/latex]

The area of any triangle is one-half of the base times the height:

[latex  latex size=”2″]\text{Area of a Triangle} = \frac{1}{2}\cdot 2a \cdot \tan\frac{\pi}{n} \cdot a[/latex]

[latex  latex size=”2″]\text{Area of a Triangle} = a^2 \tan\frac{\pi}{n}[/latex]

Finally, since the polygon has n such triangles, we’ll multiply by n:

[latex  latex size=”2″]\text{Area of a Regular Polygon} = a^{2} \cdot n \cdot \tan\frac{\pi}{n}[/latex]

Example I

Find the area of a regular octagon of side 6 mm.

A regular octagon is a polygon with eight sides. We are given the length of its side so we can use the following formula:

[latex  latex size=”2″]A = \frac{n \cdot s^{2}}{4 \ \tan \ t}[/latex]

Remember that we use n for the number of sides and s for the side length. Before plugging in n=8 and s=6, we need to find the measure of angle t.

We’ll use the formula t = ?/n , which gives us t = ?/8 . Now:

[latex  latex size=”2″]A = \frac{8 \cdot 6^{2}}{4 \cdot\tan\frac{\pi}{8}}[/latex]

[latex  latex size=”2″]A = 173.82 mm^{2}[/latex]

The area of a regular octagon of side 6 mm is approximately 174 mm².

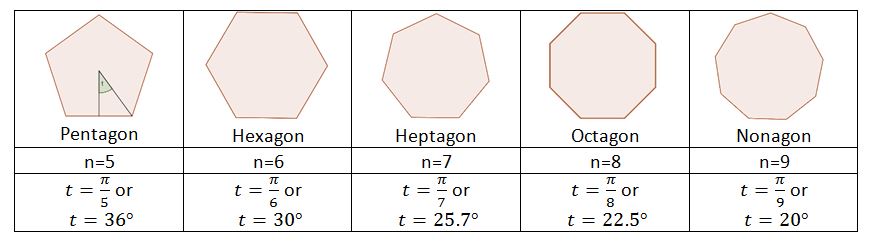
A Table of Values

In the following table, you can find some of the common polygons and the measures of the angle t, both in radians and degrees.

Example II

Find the area of a pentagon if its apothem is a=6.

Pentagon has 5 sides, so n=5 and t=?/5. We are given apothem, so we’ll use the following formula:

[latex  latex size=”2″]A = a^2 \cdot n \cdot \tan \ t[/latex]

Plug in the values into the formula to get the area:

[latex  latex size=”2″]A = 6^2 \cdot 5 \cdot \tan \frac{\pi}{5}[/latex]

[latex  latex size=”2″]A = 130.78[/latex]

The area of a pentagon whose apothem is 6 is approximately 131 square units.

To sum up

When you need to find the area of a polygon, break it down into n isosceles triangles (n is the number of sides of the polygon). Then, find the area of one triangle and multiply it by n.

[box type=”success” align=”” class=”” width=””]Want more examples? Head on over to our Geometry course for more questions and answers on Area of Polygons.[/box]