The Law of Sines (or the Sine Rule) tells us that the ratio of a side length to the sine of its opposite angle is the same for all three sides.

As a formula, it looks like this:

[latex  latex size=”3″]\frac{a}{sin\alpha}=\frac{b}{sin\beta}=\frac{c}{sin\gamma}[/latex]

or

[latex  latex size=”3″]\frac{sin\alpha}{a}=\frac{sin\beta}{b}=\frac{sin\gamma}{c}[/latex]

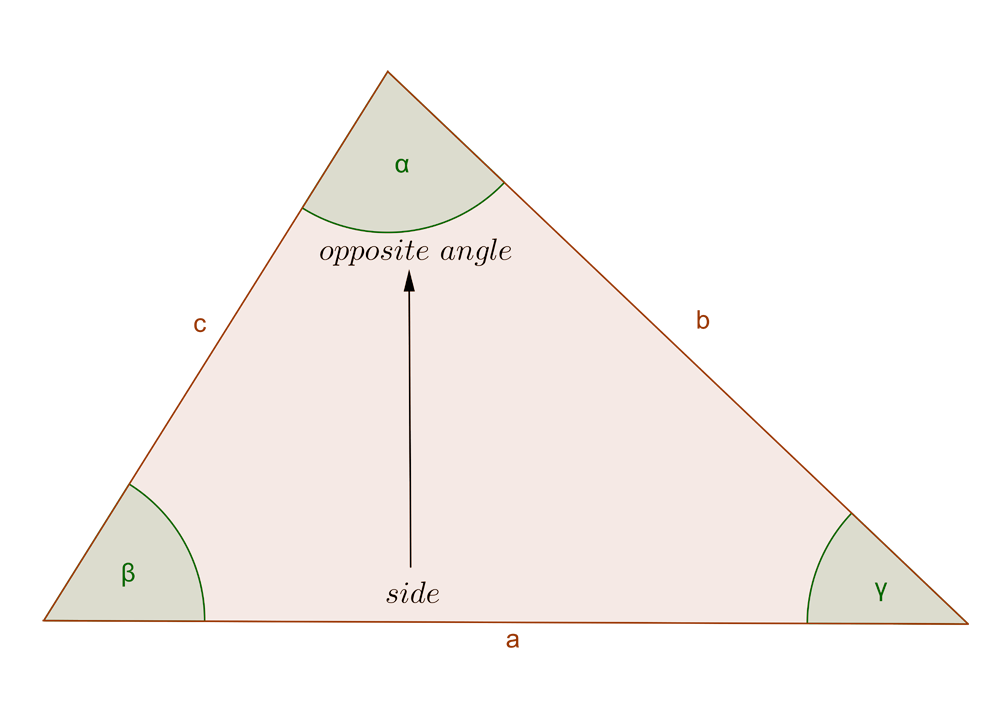
In the formula,

• a is the side and ? is its opposite angle,
• b is the side and ? is its opposite angle,
• c is the side and ? is its opposite angle

So the ratio between each of these sides and the sine of their opposite angle is the same.

The law of sines works for any triangle, unlike Sohcahtoa which works for the right-angled ones only.

Sides and angles are called the six measures of a triangle and to solve the triangle means to find all of these six measures. If we are given only some of them, we can use The Law of Sines to find the rest of them. Precisely, if we are given:

1. One side and its opposite angle
2. One or more other sides or angles

When solving problems, you won’t have to use all three ratios at the same time. Which ones you’ll take depends on what information is given about the triangle in your problem.

Example I

Find the measure of side c.

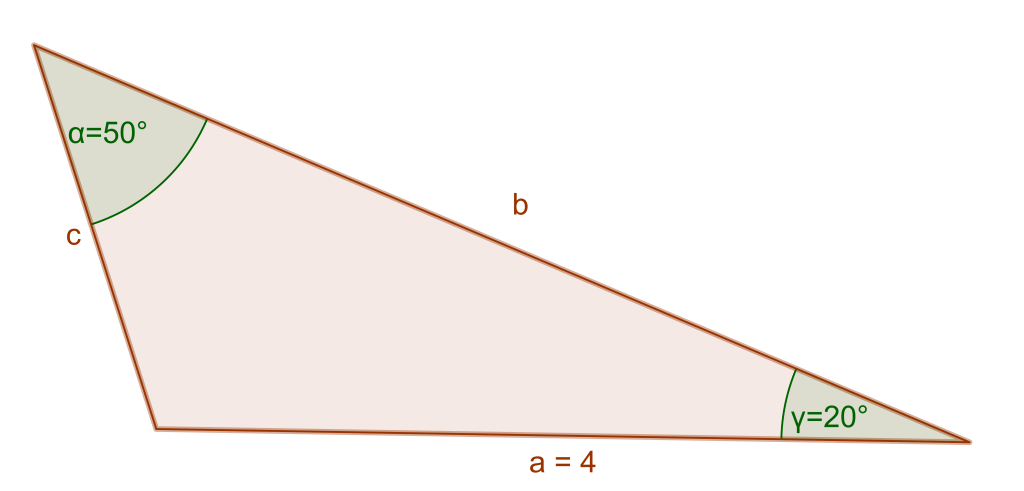
Let’s first check if we are given all that we need for The Law of Sines.

Side a and its opposite angle are there, so yes, we can apply the rule.

Looking at the information given, we’ll use the first and the last ratio from the formula:

[latex  latex size=”3″]\frac{a}{sin\alpha}=\frac{c}{sin\gamma}[/latex]

Plug in the values we have:

[latex  latex size=”3″]\frac{4}{(sin50^\circ)}=\frac{c}{(sin20^\circ)}[/latex]

Swap the sides (we want the unknown measure to be on the left):

[latex  latex size=”3″]\frac{c}{(sin20^\circ)}=\frac{4}{(sin50^\circ)}[/latex]

Multiply both sides with sin20°:

[latex  latex size=”3″]c=\frac{4}{(sin50\circ)}*sin20^\circ[/latex]

And now calculate using your calculator:

[latex  latex size=”3″]c=\frac{4}{0.766}*0.342[/latex]

[latex  latex size=”3″]c=1.786[/latex]

[latex  latex size=”3″]c=1.9 \text{(to one decimal place)}[/latex]

Example II

Find the missing angle ?.

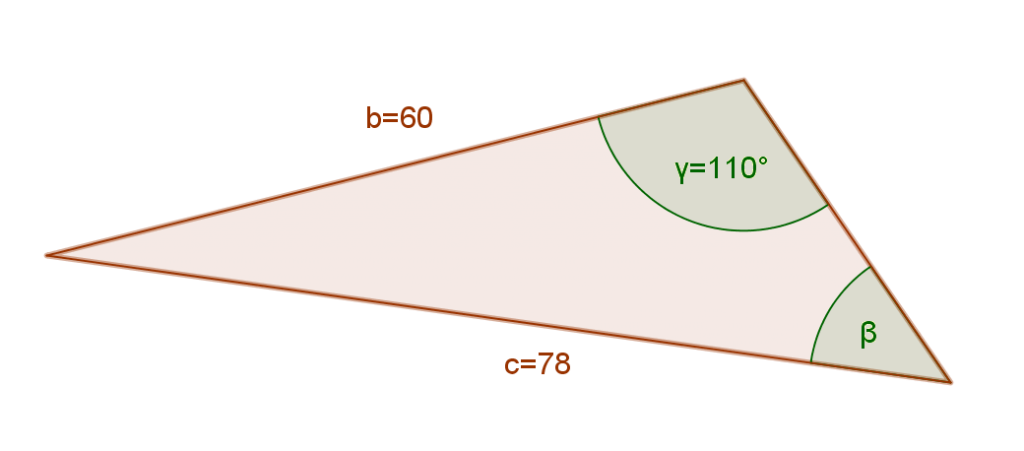
We are given a side c and its opposite angle, so we can apply the Sine Rule. When you need to find the missing angle, it’s best to use the second formula:

[latex  latex size=”3″]\frac{sin\gamma}{c}=\frac{sin\beta}{b}[/latex]

Plug in the values we have:

[latex  latex size=”3″]\frac{(sin110^\circ)}{78}=\frac{sin\beta}{60}[/latex]

Swap the sides to get the unknown angle to the left side:

[latex  latex size=”3″]\frac{sin\beta}{60}=\frac{(sin110^\circ)}{78}[/latex]

Multiply both sides with 60:

[latex  latex size=”3″]sin\beta=\frac{(sin110^\circ)}{78}*60[/latex]

And now use the calculator to solve the right side of this equation:

[latex  latex size=”3″]sin\beta=\frac{0.940}{78}*60[/latex]

[latex  latex size=”3″]sin\beta=0.806[/latex]

Finally, find the inverse of the sine:

[latex  latex size=”3″]\beta=sin^{-1}[/latex]  [latex  latex size=”3″]0.806[/latex]

[latex  latex size=”3″]\beta=53.7^\circ[/latex]

How would you find the third side?

Let’s solve this triangle completely, i.e. let’s find the remaining side and angle.

To find the angle we’ll use the property that the sum of interior angles in a triangle is 180°:

[latex  latex size=”3″]\alpha+\beta+\gamma=180^\circ[/latex]

[latex  latex size=”3″]\alpha+53.7^\circ+110^\circ=180^\circ[/latex]

[latex  latex size=”3″]\alpha+163.7^\circ=180^\circ[/latex]

[latex  latex size=”3″]\alpha=180^\circ-163.7^\circ[/latex]

[latex  latex size=”3″]\alpha=16.3^\circ[/latex]

Now we can set up the equation to find the side a, using the Sine Rule:

[latex  latex size=”3″]\frac{a}{sin\alpha}=\frac{b}{sin\beta}[/latex]

[latex  latex size=”3″]\frac{a}{(sin16.3^\circ)}=\frac{60}{(sin53.7^\circ)}[/latex]

[latex  latex size=”3″]a=\frac{60}{(sin53.7^\circ)}*sin16.3^\circ[/latex]

[latex  latex size=”3″]a=\frac{60}{0.806}*0.281[/latex]

[latex  latex size=”3″]a=20.918[/latex]

[latex  latex size=”3″]a=20.9[/latex]

Example III

Solve the triangle below.

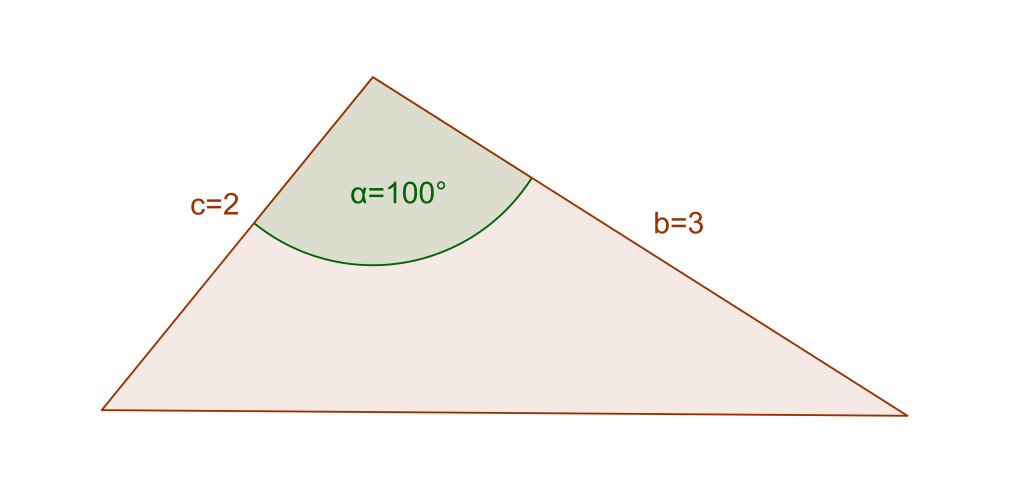
Let’s first check if we can apply the Sine Rule here.

We are given side b but not its opposite angle. Also, we are given side c but not its opposite angle. Therefore, we can’t apply the formula. This triangle is not suited for The Law of Sines (but it is for The Law of Cosines).

The Ambiguous Case

The ambiguous case comes from the fact that an acute angle and an obtuse angle have the same sine (check the Unit Circle). For example, sin30°=1/2 and sin150°=1/2.

Let us use the Law of Sines to find angle ?.

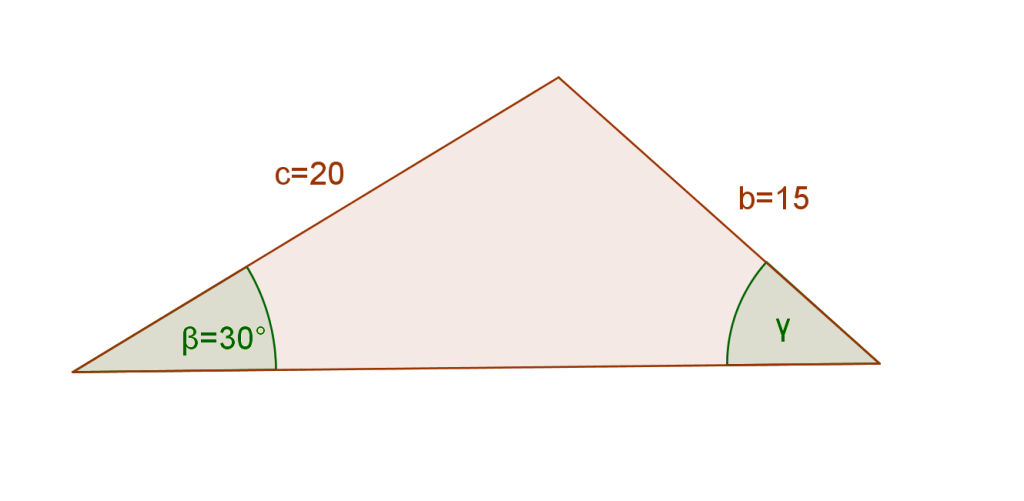
[latex  latex size=”3″]\frac{sin\beta}{b}=\frac{sin\gamma}{c}[/latex]

[latex  latex size=”3″]\frac{sin30^\circ}{15}=\frac{sin\gamma}{20}[/latex]

[latex  latex size=”3″]\frac{sin\gamma}{20}=\frac{sin30^\circ}{15}[/latex]

[latex  latex size=”3″]sin\gamma=\frac{sin30^\circ}{15}*20[/latex]

The sine of 30° is 1/2:

[latex  latex size=”3″]sin\gamma=\frac{\frac{1}{2}}{15}*20[/latex]

[latex  latex size=”3″]sin\gamma=\frac{10}{15}[/latex]

[latex  latex size=”3″]sin\gamma=\frac{2}{3}[/latex]

[latex  latex size=”3″]sin\gamma=0.667[/latex]

[latex  latex size=”3″]\gamma=sin^{-1}[/latex]  ?[latex  latex size=”3″]0.667[/latex]

[latex  latex size=”3″]\gamma\approx 42^\circ[/latex]

However, angle 138° has the same sine as angle 42°, i.e. sin138°=0.667, so this problem has two solutions.

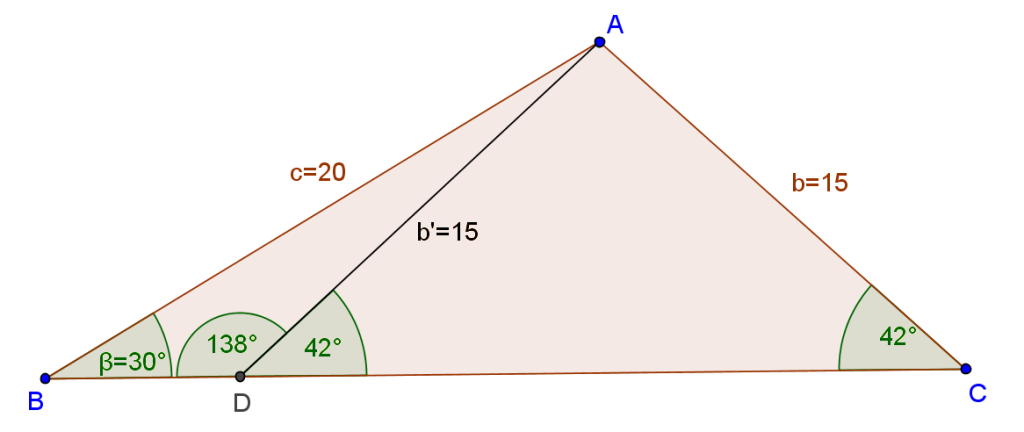
Not only is angle ?BCA a solution, but so is angle ?BDA.

However, this won’t always be the case. Sometimes you’ll have two possible solutions and sometimes one, so you should always check if the other solution makes sense.

The Circumcircle Connection

The Law of Sines tells us that the ratio between the sides and their opposite angles is the same. Additionally, that ratio is also the diameter of the circumcircle, which is the circle that passes through all three vertices of the triangle:

[latex  latex size=”3″]\frac{a}{sin\alpha}=\frac{b}{sin\beta}=\frac{c}{sin\gamma}=2r[/latex]

where r is the radius of the triangle’s circumcircle.

Summary

If we are given one side and its opposite angle we can apply the Law of Sines formula and then, using other given elements, we can solve the triangle.

[box type=”success” align=”” class=”” width=””]Did this help? You can view more examples in Trigonometry + 100 other subjects at Educator.com, the best place to get in-depth and instant homework help online.[/box]