We have already seen how to solve triangles using the Law of Sines. Such problems involve two sides and two angles. The Law of Cosines (or the Cosine Rule) is used when we have all three sides involved and only one angle. The formula is:

[latex  latex size=”3″]c^{2} = a^{2} + b^{2} – 2ab\text{cos}y[/latex]

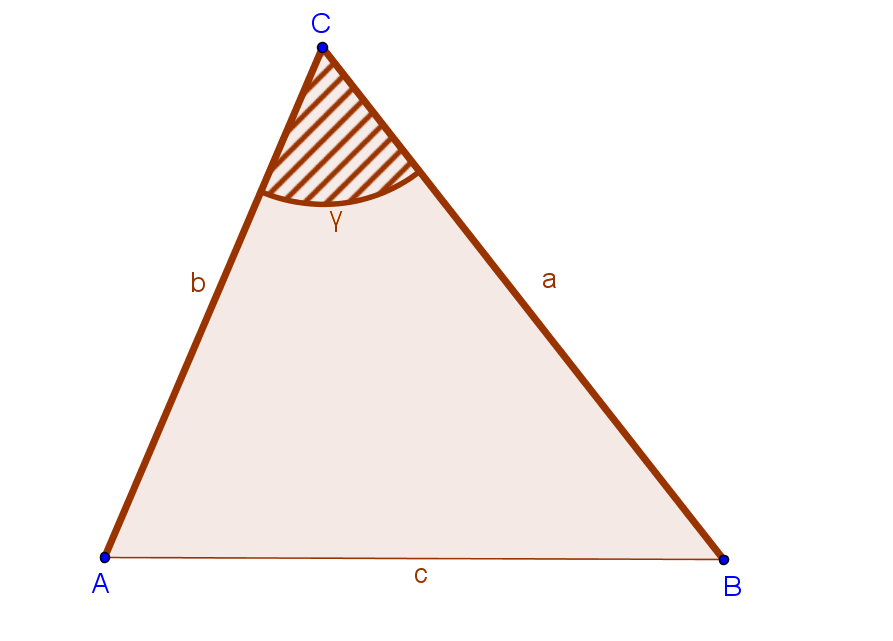
• c is the unknown side
• a and b are the given sides
• ? is not any angle in the triangle, but the angle between the given sides.

We use the Law of Cosines to solve triangles that are not right-angled.

How to remember

This rule is very similar to the Pythagorean theorem. If angle ? were a right angle, we would have

 [latex  latex size=”3″]c^2 = a^2 + b^2 – 2ab\text{cos}90^\circ[/latex]

We know that cos90°=0, so the equation above becomes

 [latex  latex size=”3″]c^2 = a^2 + b^2 – 0[/latex]

 [latex  latex size=”3″]c^2 = a^2 + b^2[/latex]

which is actually the Pythagorean theorem.

We can write the Law of Cosines for each angle in the triangle, following the pattern (two given sides and the angle between them):

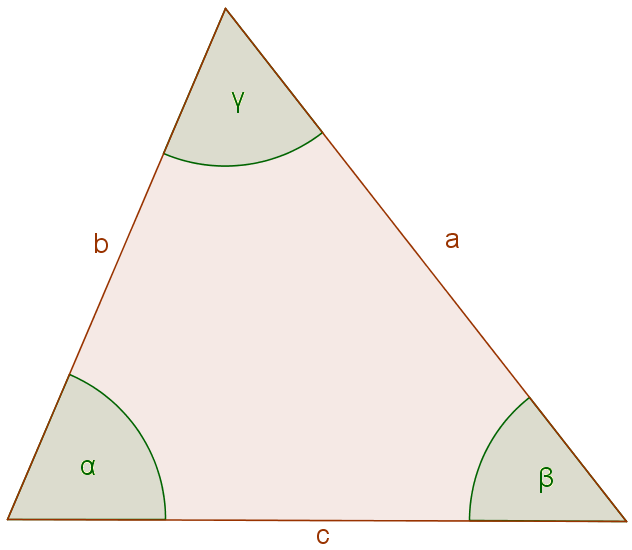
[latex  latex size=”3″]a^2 = b^2 + c^2 – 2bc\text{cos}\alpha[/latex]

[latex  latex size=”3″]b^2 = a^2 + c^2 – 2ac\text{cos}\beta[/latex]

[latex  latex size=”3″]c^2 = a^2 + b^2- 2ab\text{cos}\gamma[/latex]

You don’t need to memorize all these formulas; it is important just to understand the rule and know the pattern.

Sometimes we are given all the three sides, and we need to find the angle. In that case, we can rearrange the formula above to get:

 [latex  latex size=”3″]\text{cos}\gamma = \frac{a^2+b^2-c^2}{2ab}[/latex]

Example I

Find the missing side in the triangle below.

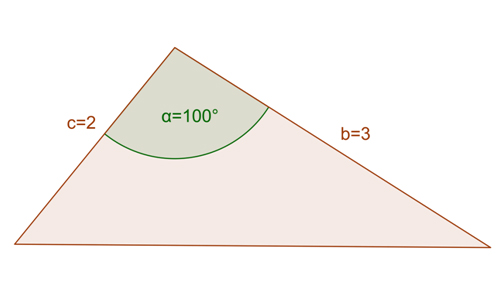
We are given side b=3 and side c=2. The angle between them is 100°. We need to find the length of the missing side, so let’s put the given information into the formula:

[latex  latex size=”3″]a^2 = b^2 + c^2 – 2bc\text{cos}\alpha[/latex]

[latex  latex size=”3″]a = 3^2 + 2^2 – 2*3*2\text{cos}100^\circ[/latex]

[latex  latex size=”3″]a = 9 + 4 – 12 * (-0.17)[/latex]

[latex  latex size=”3″]a =15.04[/latex]

Example II

Find the largest angle of a triangle whose sides are 12, 16 and 9.

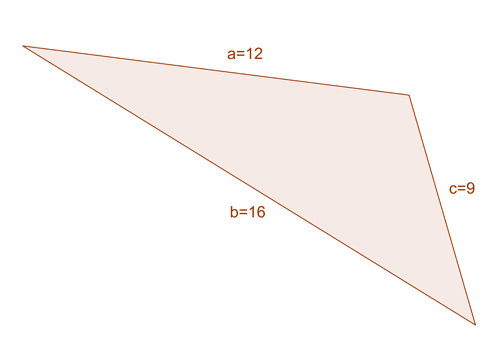
The largest angle of a triangle is the one opposite to the largest side. In the triangle above, the largest side is b so we’ll find the measure of angle ?.

We can use the second formula

 [latex  latex size=”3″]\text{cos}\beta = \frac{a^2+c^2-b^2}{2ac}[/latex]

 [latex  latex size=”3″]\text{cos}\beta = \frac{12^2+9^2-16^2}{2*12*9}[/latex]

 [latex  latex size=”3″]\text{cos}\beta = \frac{144+81-256}{216}[/latex]

 [latex  latex size=”3″]\text{cos}\beta = -\frac{31}{216}[/latex]

 [latex  latex size=”3″]\text{cos}\beta = -0.1435[/latex]

 [latex  latex size=”3″]\beta = cos^{-1}(-0.1435)[/latex]

 [latex  latex size=”3″]\beta = 98.25^\circ[/latex]

Example III

Use the Law of Cosines to find the length of the missing side.

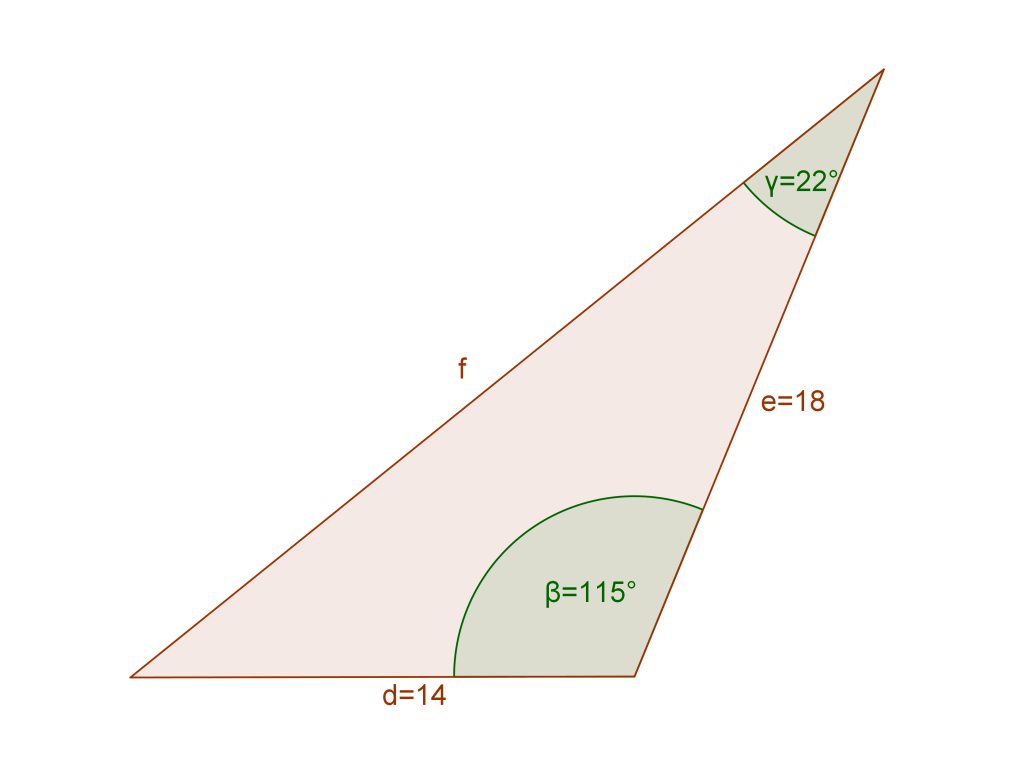
To apply the Law of Cosines in this problem, we need two sides and the angle between them. So don’t let the 22° angle confuse you. It does nothing for you here.

Since we need to find the missing side, we’ll use the formula:

 [latex  latex size=”3″]f^2 = d^2 + e^2 -2de\text{cos}\beta[/latex]

Don’t let the different letters confuse you either! Both d and e are the given sides, and ? is the angle between them, while f is the unknown side.

 [latex  latex size=”3″]f^2 = 14^2 + 18^2 -2*14*18*\text{cos}115^\circ[/latex]

 [latex  latex size=”3″]f^2 = 196+ 324 – 504 *(-0.4226)[/latex]

 [latex  latex size=”3″]f^2 = 520 + 212.99[/latex]

 [latex  latex size=”3″]f^2 = 732.99[/latex]

 [latex  latex size=”3″]f = 27.07[/latex]

Summary

We use the Law of Cosines to solve triangles in two cases:

1. We are given two sides and the angle between them
2. We are given all three sides

We need to be careful – the formula works only if the angle given is the included angle.

[box type=”success” align=”” class=”” width=””]Want to learn more? Check out more examples in Trigonometry + 100 other subjects at Educator.com, the best place to get in-depth and instant homework help online. [/box]