In Physics, motion is always described from the point of view of an observer. If two observers are moving different manners, they might observe the same event in differently.

Lets see a very simple example.

Say you are on a train, which is moving with a constant velocity – ‘v’ . Lets say a cat is sitting on a chair in front of you. So for you this cat is stationary.

But if a person from outside the train observes, he or she will see this cat moving away at the same speed – ‘v’as the train!

Thus the motion is always relative to the reference frame of an observer. This is where the concept of Reative Motion arises.

What is a Reference Frame?

A reference frame is the co-ordinate system that the observer uses to measure motion. It moves in the same manner as the observer.

A reference frame describe the motion of an observer.

For the time being we will deal with only reference frames which are inertial, which means they are non-accelerating. The laws of physics observed from all inertial reference frames are same.

Since most of the motion we are concerned with takes place on the surface of our planet, earth is the most common reference frame.

*technically earth in not inertial since it is rotating around its axis, revolving around the sun, etc. But these make so little difference most of the time, that for present purposes we will consider it as an inertial, non-accelerating frame of reference.

Another important point to note is that it is impossible to figure out whether motion of an object is being observed from a stationary reference frame or a frame moving in constant velocity, by just observing the motion of the object.

For example, say a plane is stationary on the ground without any movement and you dribble a basketball inside the plane.

Now say you are on the plane and it is flying very smoothly (without any turbulence) and you again dribble the basketball.

You will not be able to notice any difference and if all the windows are closed, you won’t be able to tell if the plane is flying or is stationary just by observing the motion of the basketball.

Relative Motion

For the reasons we have discussed this far, we never talk about absolute motion. Whenever we talk about motion in physics, it is always relative to an observer or a frame of reference.

An observer is always stationary in his/her own reference frame and everything else moves or is at rest with respect to this reference frame.

Remember the reference frame can be considered a co-ordinate system that is moving along with the observer!

Lets take an example to understand relative motion.

Say there are two cars. Car-A (at the leftmost end) and car-B(at the rightmost end) .

Car-A is stationary but car-B is moving at a constant velocity of 50m/s to the left towards car-A according to an observer on the ground.

Now if we take car-A to be the observer, then car-B will be moving at 50m/s towards car -A, i.e. to the left.

As we can see the picture, the position of car-B changes as it moves to the left on the co-ordinate system of car-A.

But, what if we take car-B to be the observer?

Remember that observers are always at rest in their own reference frame.

So we see the co-ordinate system of car-B moves with it when car-B moves to the left, and thus the position of car-A on this co-ordinate system changes from point-p1 to point-p2!

You will also notice that since the co-ordinate system moves along with car-B, its own position never changes on this co-ordinate system!

So car-B will see car-A moving towards car-B at 50m/s. So for car-B , car-A is moving towards the right with 50m/s

This concept of moving co-ordinate system will play an important part in understanding Einsten’s Theory of Relativity

Calculation of relative velocities

Example1:

Now let us go back to our very first example with the cat, the train and an observer on the ground.

Lets say the train is moving towards the east. The the cat is also walking away on the train towards the east.

Let us denote: the cat as A

The train as B

and The observer on the ground as C

The velocity of the cat with respect to the train is

The velocity of the cat with respect to ground observer is

The velocity of the train with respect to ground observer is

Then we calculate relative velocity of the cat with respect to the ground observer as

So to find the velocity of the cat with respect to the ground observer, we need to add the velocity of the cat with respect to the train and the velocity of the train with respect to the ground observer.

NOTE: If instead of three (as in this example), there are four entities involved, we can simply calculate the relative velocities as

This can be stretched to as many entities/observers/reference frames as you want.

Example2:

Lets see another example.

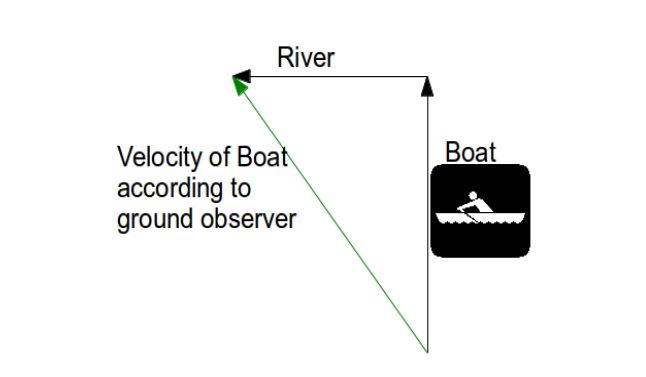
Say a boat is moving to the north at 4m/s on a river. An observer on the ground can see that the river itself is flowing to the west at 3m/s. What would be the speed of the boat according to the ground observer ?

ANS-

Let us denote: the boat as A

The river as B

and The observer on the ground as C

So as we saw earlier –

The relative velocity of the boat with respect to the ground observer is

Now if add the velocities in vector form (the magnitude according to Pythagorean theorem)

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our AP Physics 1 & 2 course. We cover topics such as Relative Motion.[/box]