What is a projectile?

A projectile is any object which is only acted upon by the force of gravity.

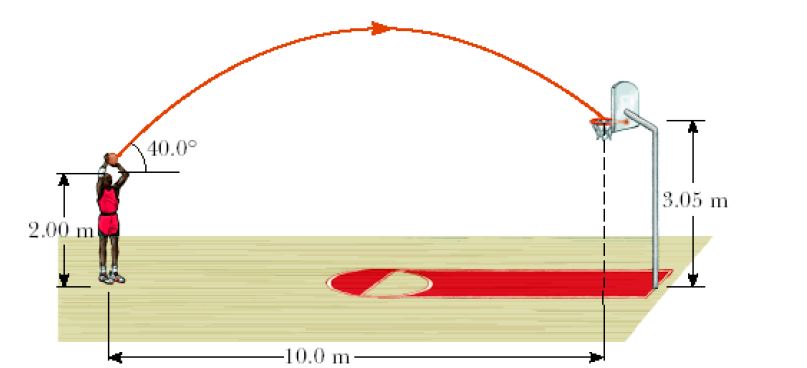
A ball thrown in the air for example is an example of projectile. We can see examples of projectile motion in our day to day life. Objects falling down, objects thrown around, etc. are all example of projectiles.

You can an example of projectile motion of the basketball in the above picture.

In reality, since it moves through the air, force in the form of air resistance is also present. But we will neglect air resistance and assume that only the force of gravity is acting on it.

We will now study and analyse the path taken by a projectile.

Path of a projectile

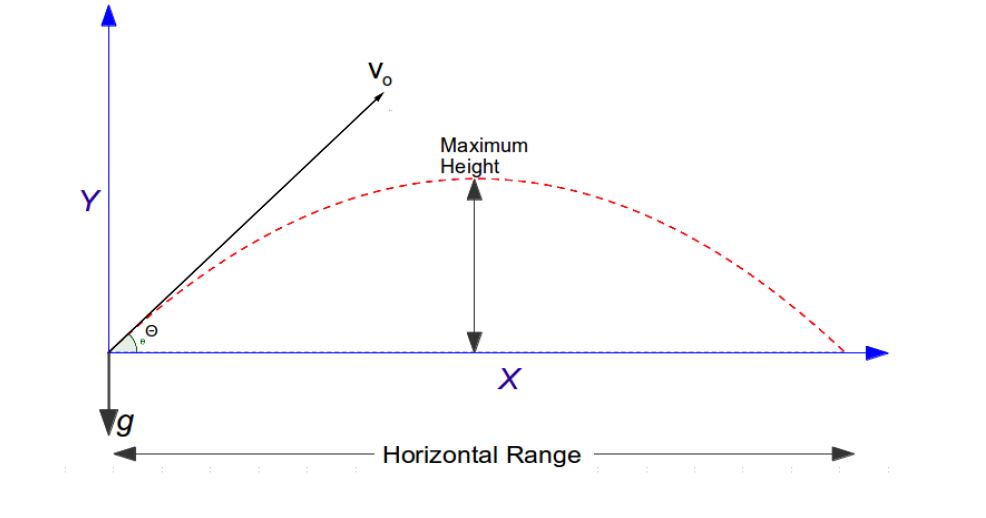
Projectiles when launched at an angle follow parabolic path.

Gravitational force is responsible for acceleration. Thus all projectiles experience acceleration due to gravity –> g. This affects the path of a projectile.

The path of the projectile also depends on the angle with which it is thrown or projected and the initial velocity (v_o). Almost all of us have experienced that while throwing objects!

Thus we can see that projectiles thrown at an angle with some initial velocity follow a parabolic arc.

It reaches certain height and then starts falling back towards the ground. The highest point it can reach is known as the maximum height of the projectile.

The projectile covers certain distance before it comes to a rest. This distance covered on the x-axis is known as horizontal range of the projectile.

We can also notice that if the projectile falls back to the same height from where it was launched, then the path taken to ascend to the maximum height is the mirror image of the path taken by the projectile to descend. Thus it is symmetric.

Independence of motion

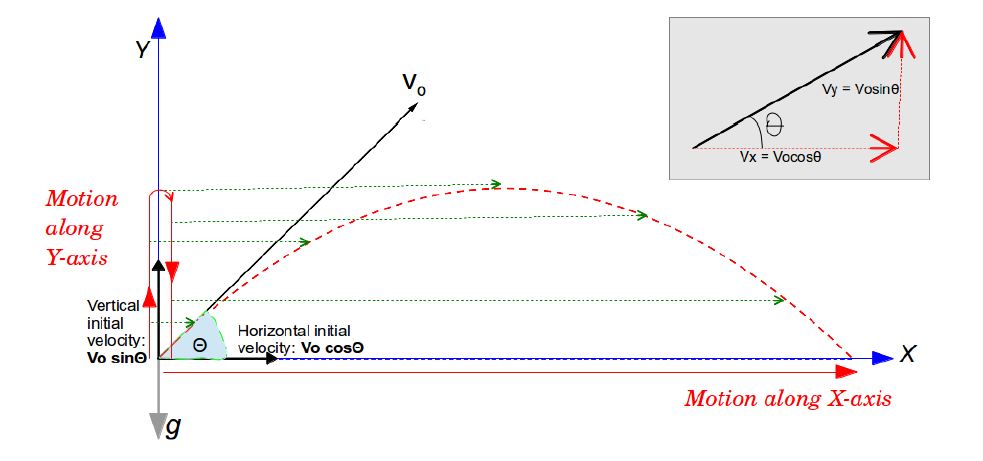
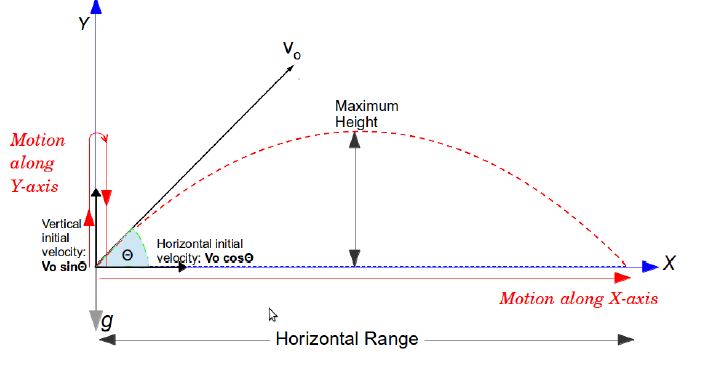
Projectile motion takes place in 2 dimensions. Let’s say it is thrown with an initial velocity Vo at an angle ?.

In the Y-axis

• projectile has initial velocity ‘Vo sin?’ (vertical component of Vo )
• and is acted upon by free fall acceleration – g, in the downwards direction.
• So the motion along Y-axis is that of simple ‘free fall’.

In the X-axis

• Projectile has initial velocity ‘Vo cos?’ (horizontal component of Vo).
• There is no acceleration in the horizontal direction, so the velocity along X-axis is constant.

One important point we need to remember is that, free fall acceleration is always vertically downwards. Since it has no components in the horizontal direction, it only affects motion along the Y-axis

We will use the Kinematic equations, in the two independent axis (X and Y separately), to analyze the projectile motion.

Projectiles at an angle

Let us now analyze the general case of projectiles at angle.

For projectiles thrown at an angle, we can find the maximum height, time of flight (amount of time the projectile is in the air) and horizontal range.

(You can revise the Kinematic equations from the previous chapter before going through the next section.)

• Lets have a look at horizontal range.

There is no acceleration along the x-axis. So the horizontal component of the initial velocity(Vo cos?) will not change.

So the range or displacement is –

 
 

 
 
Since,

Time of flight simply the amount of time the projectile spends in air, before it hits the ground again.

Now, to find the time of flight we need to figure the motion along Y-axis. After which we can figure out horizontal range!

• So lets have a look at the motion along the Y-axis and then we can come back to formulating the range, once we find the time of flight.

Along Y-axis –

Vertical initial velocity: V_o sin?

(Since the vertical component of initial velocity is upwards, we can take it as the positive direction.)

Acceleration : -g (downward direction)

So lets calculate first the time taken to reach maximum height along Y-axis.

Horizontal component of velocity at maximum height = 0

So we use the equation –

 
 

 
 

 
 

 
 
Now we can find out the time of flight using the fact that motion is symmetric. Which means that the time taken by the projectile to reach the maximum height is the same as time taken by it to fall back to the its origin.

So time of flight is simply twice the time taken to reach its maximum height.

So,

NOTE: An alternative approach could have been to use the folowing equation:

Where we take ?x = 0 (Since it comes back to the same point on Y-axis)

and initial velocity = V_osin?

So,

 
 
=
 
 

 
 

Since t=0 denotes the case where the projectile doesn’t move along the Y-axis at all, we ignore it.

So we end up with the same expression with a slightly different method.
So, time of flight is:

• Next we figure out the maximum height

 
 
For this purpose we use the equation

We know at maximum height the Vertical component of velocity is 0.

Initial vertical velocity = V_o sin?

acceleration = -g

So, ?x will give us maximum height.

Then,

 
 

 
 

 
 

 
 
So maximum height is:

• Back to Horizontal Range !

So horizontal range was

Now we know,
 
 

So,
 
 

(Using trigonometric identities)

• Now we can see that if we vary the angle, the range of projectile will change.

If we want to launch it, so that it covers maximum range, we need to select an angle such that sin2? is maximum.

Now we know that, highest value the sine function can take is 1.

So, sin2? =1, will give us maximum range!

So,

So if we throw a projectile at 45^o angle, it will have the maximum range!

Motion Graphs

Suppose a projectile is thrown at an angle of 45^o , and after tracing a parabolic path, falls back to the same height.

Let us see how the ‘acceleration vs time’, ‘velocity vs time’ and ‘displacement vs time’ graphs would look.

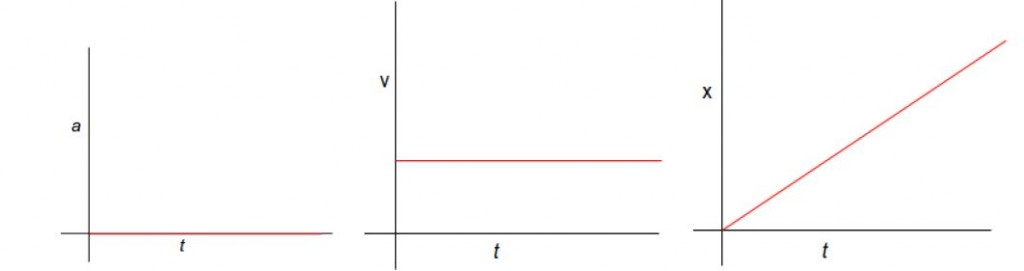
Let us first look at motion along the X-axis:

• Since no acceleration is there along the X-axis, the first graph is at zero throughout.
• The velocity along X-axis is constant since there is no acceleration.
• The displacement is linearly increasing with time.

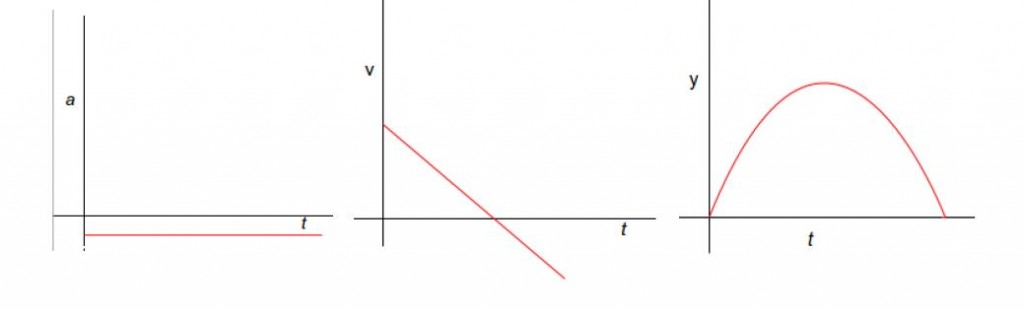
Now let us look at motion along the Y-axis:

• Now we can see constant acceleration along Y-axis. That is the free fall acceleration (g) . It is negative because we took upwards as the positive direction. It could very much be positive if we choose downward direction as positive.
• Since acceleration is constant, velocity changes linearly with time. The velocity along Y-axis starts with a positive value. At maximum height it becomes zero and then has negative value after that.
• The displacement starts from zero, reaches maximum height, and then again reduces back to zero.

Now that we have analysed the projectile motion in general, let us see an example.

Examples

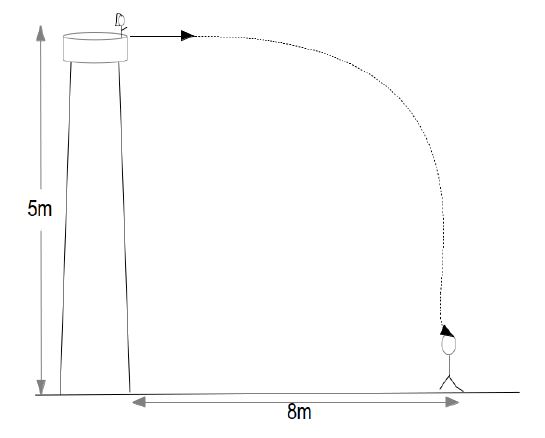
Q1) Alice who is standing on top of a Tower 5m tall, throws a heavy ball horizontally. How fast should Alice throw it so that it reaches Bob who is standing 8meter away from the base of the tower on the ground. [Assume g=10m/s²]

ANS) Now since ball is thrown horizontally, the initial vertical velocity is zero.

So,

Vy = 0m/s (initial vertical velocity)

?y = -5 (taking downward direction as negative)

a = -g

 
 

 
 

 
 

 
 

 
 

So the ball will remain in air for 1sec

Now lets say horizontal velocity at which ball is thrown = Vx

and ?x = 8m

So,

 
 

 
 

 
 

 
 
So , the ball should be thrown at 8m/s

[box type=”success” align=”” class=”” width=””]For more examples check out some of the lessons in our AP Physics 1 & 2 course. We cover topics such as Projectiles.[/box]