

Professor Murray
Trapezoidal Rule, Midpoint Rule, Left/Right Endpoint Rule
Slide Duration:Table of Contents
24m 52s
- Intro0:00
- Important Equation0:07
- Where It Comes From (Product Rule)0:20
- Why Use It?0:35
- Lecture Example 11:24
- Lecture Example 23:30
- Shortcut: Tabular Integration7:34
- Example7:52
- Lecture Example 310:00
- Mnemonic: LIATE14:44
- Ln, Inverse, Algebra, Trigonometry, e15:38
- Additional Example 4-1
- Additional Example 5-2
25m 30s
- Intro0:00
- Important Equation0:07
- Powers (Odd and Even)0:19
- What To Do1:03
- Lecture Example 11:37
- Lecture Example 23:12
- Half-Angle Formulas6:16
- Both Powers Even6:31
- Lecture Example 37:06
- Lecture Example 410:59
- Additional Example 5-1
- Additional Example 6-2
30m 9s
- Intro0:00
- Important Equations0:06
- How They Work0:35
- Example1:45
- Remember: du and dx2:50
- Lecture Example 13:43
- Lecture Example 210:01
- Lecture Example 312:04
- Additional Example 4-1
- Additional Example 5-2
41m 22s
- Intro0:00
- Overview0:07
- Why Use It?0:18
- Lecture Example 11:21
- Lecture Example 26:52
- Lecture Example 313:28
- Additional Example 4-1
- Additional Example 5-2
20m
- Intro0:00
- Using Tables0:09
- Match Exactly0:32
- Lecture Example 11:16
- Lecture Example 25:28
- Lecture Example 38:51
- Additional Example 4-1
- Additional Example 5-2
22m 36s
- Intro0:00
- Trapezoidal Rule0:13
- Graphical Representation0:20
- How They Work1:08
- Formula1:47
- Why a Trapezoid?2:53
- Lecture Example 15:10
- Midpoint Rule8:23
- Why Midpoints?8:56
- Formula9:37
- Lecture Example 211:22
- Left/Right Endpoint Rule13:54
- Left Endpoint14:08
- Right Endpoint14:39
- Lecture Example 315:32
- Additional Example 4-1
- Additional Example 5-2
21m 8s
- Intro0:00
- Important Equation0:03
- Estimating Area0:28
- Difference from Previous Methods0:50
- General Principle1:09
- Lecture Example 13:49
- Lecture Example 26:32
- Lecture Example 39:07
- Additional Example 4-1
- Additional Example 5-2
44m 18s
- Intro0:00
- Horizontal and Vertical Asymptotes0:04
- Example: Horizontal0:16
- Formal Notation0:37
- Example: Vertical1:58
- Formal Notation2:29
- Lecture Example 15:01
- Lecture Example 27:41
- Lecture Example 311:32
- Lecture Example 415:49
- Formulas to Remember18:26
- Improper Integrals18:36
- Lecture Example 521:34
- Lecture Example 6 (Hidden Discontinuities)26:51
- Additional Example 7-1
- Additional Example 8-2
23m 20s
- Intro0:00
- Important Equation0:04
- Why It Works0:49
- Common Mistake1:21
- Lecture Example 12:14
- Lecture Example 26:26
- Lecture Example 310:49
- Additional Example 4-1
- Additional Example 5-2
28m 53s
- Intro0:00
- Important Equation0:05
- Surface Area0:38
- Relation to Arclength1:11
- Lecture Example 11:46
- Lecture Example 24:29
- Lecture Example 39:34
- Additional Example 4-1
- Additional Example 5-2
24m 37s
- Intro0:00
- Important Equation0:09
- Main Idea0:12
- Different Forces0:45
- Weight Density Constant1:10
- Variables (Depth and Width)2:21
- Lecture Example 13:28
- Additional Example 2-1
- Additional Example 3-2
25m 39s
- Intro0:00
- Important Equation0:07
- Main Idea0:25
- Centroid1:00
- Area1:28
- Lecture Example 11:44
- Lecture Example 26:13
- Lecture Example 310:04
- Additional Example 4-1
- Additional Example 5-2
22m 26s
- Intro0:00
- Important Equations0:05
- Slope of Tangent Line0:30
- Arc length1:03
- Lecture Example 11:40
- Lecture Example 24:23
- Lecture Example 38:38
- Additional Example 4-1
- Additional Example 5-2
30m 59s
- Intro0:00
- Important Equations0:05
- Polar Coordinates in Calculus0:42
- Area0:58
- Arc length1:41
- Lecture Example 12:14
- Lecture Example 24:12
- Lecture Example 310:06
- Additional Example 4-1
- Additional Example 5-2
31m 13s
- Intro0:00
- Definition and Theorem0:05
- Monotonically Increasing0:25
- Monotonically Decreasing0:40
- Monotonic0:48
- Bounded1:00
- Theorem1:11
- Lecture Example 11:31
- Lecture Example 211:06
- Lecture Example 314:03
- Additional Example 4-1
- Additional Example 5-2
31m 46s
- Intro0:00
- Important Definitions0:05
- Sigma Notation0:13
- Sequence of Partial Sums0:30
- Converging to a Limit1:49
- Diverging to Infinite2:20
- Geometric Series2:40
- Common Ratio2:47
- Sum of a Geometric Series3:09
- Test for Divergence5:11
- Not for Convergence6:06
- Lecture Example 18:32
- Lecture Example 210:25
- Lecture Example 316:26
- Additional Example 4-1
- Additional Example 5-2
23m 26s
- Intro0:00
- Important Theorem and Definition0:05
- Three Conditions0:25
- Converging and Diverging0:51
- P-Series1:11
- Lecture Example 12:19
- Lecture Example 25:08
- Lecture Example 36:38
- Additional Example 4-1
- Additional Example 5-2
22m 44s
- Intro0:00
- Important Tests0:01
- Comparison Test0:22
- Limit Comparison Test1:05
- Lecture Example 11:44
- Lecture Example 23:52
- Lecture Example 36:01
- Lecture Example 410:04
- Additional Example 5-1
- Additional Example 6-2
25m 26s
- Intro0:00
- Main Theorems0:05
- Alternation Series Test (Leibniz)0:11
- How It Works0:26
- Two Conditions0:46
- Never Use for Divergence1:12
- Estimates of Sums1:50
- Lecture Example 13:19
- Lecture Example 24:46
- Lecture Example 36:28
- Additional Example 4-1
- Additional Example 5-2
33m 27s
- Intro0:00
- Theorems and Definitions0:06
- Two Common Questions0:17
- Absolutely Convergent0:45
- Conditionally Convergent1:18
- Divergent1:51
- Missing Case2:02
- Ratio Test3:07
- Root Test4:45
- Lecture Example 15:46
- Lecture Example 29:23
- Lecture Example 313:13
- Additional Example 4-1
- Additional Example 5-2
38m 36s
- Intro0:00
- Main Definitions and Pattern0:07
- What Is The Point0:22
- Radius of Convergence Pattern0:45
- Interval of Convergence2:42
- Lecture Example 13:24
- Lecture Example 210:55
- Lecture Example 314:44
- Additional Example 4-1
- Additional Example 5-2
30m 18s
- Intro0:00
- Taylor and Maclaurin Series0:08
- Taylor Series0:12
- Maclaurin Series0:59
- Taylor Polynomial1:20
- Lecture Example 12:35
- Lecture Example 26:51
- Lecture Example 311:38
- Lecture Example 417:29
- Additional Example 5-1
- Additional Example 6-2
50m 50s
- Intro0:00
- Main Formulas0:06
- Alternating Series Error Bound0:28
- Taylor's Remainder Theorem1:18
- Lecture Example 13:09
- Lecture Example 29:08
- Lecture Example 317:35
- Additional Example 4-1
- Additional Example 5-2
For more information, please see full course syllabus of College Calculus: Level II
College Calculus: Level II Trapezoidal Rule, Midpoint Rule, Left/Right Endpoint Rule
In this tutorial we are going to discuss three methods of integration approximation, the Trapezoidal Rule, the Midpoint Rule, and the Left/Right Endpoint Rule. What we are going to try to do is find approximation techniques that do not rely on us being able to take the integral. The idea for all of these techniques is the same: we have a function that we want to integrate from a to b, and we start out by dividing the region between a to b into n equal partitions. So, first, we are going to talk about Trapezoidal rule. We will see graphical explanation of it, how it works and its formula. The same pattern will be used for other rules.
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
- - Allow users to view the embedded video in full-size.










































 Answer Engine
Answer Engine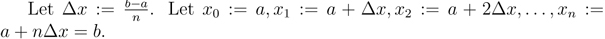
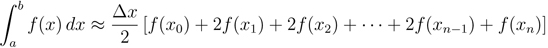
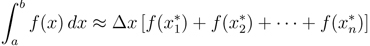
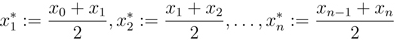
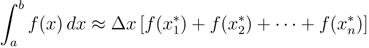
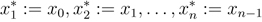
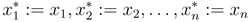






1 answer
Fri Jun 27, 2014 4:59 PM
Post by Jorge Sardinas on June 24, 2014
Dear Dr.Murray
thank for all the wonderful lectures and i just wanted to let you know that you are an amazing teacher
P.S. I also love your trigonometry lessons.
1 answer
Tue Jan 7, 2014 11:29 AM
Post by Edmund Mercado on December 20, 2013
Dr. Murray:
Isn't the calculator required to be in radian mode for these solutions?
1 answer
Mon Nov 12, 2012 4:47 PM
Post by Justin Malaer on November 10, 2012
Do you guys even answer questions?
1 answer
Tue May 14, 2013 9:55 AM
Post by Jess Wood on October 15, 2011
In the last example of the left endpoint rule, there is a 1/2 that is multiplied throughout the added height of the left endpoints. Is that 1/2 suppose to be 1/4? If not how did the 1/2 come about?